Höfundur:
Robert Simon
Sköpunardag:
21 Júní 2021
Uppfærsludagsetning:
1 Júlí 2024
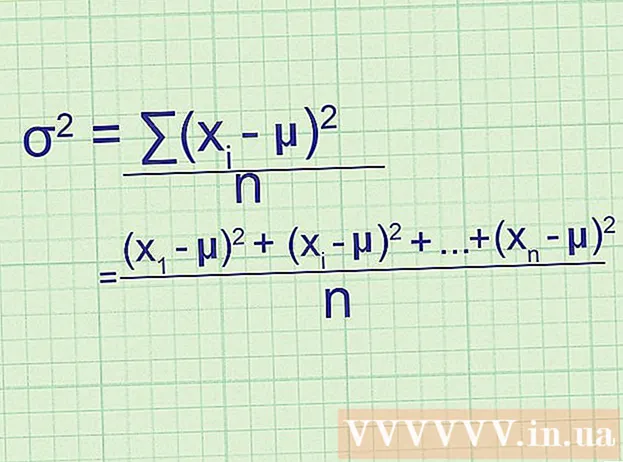
Efni.
Afbrigði mælir dreifingu gagnasafnsins. Það er mjög gagnlegt við uppbyggingu tölfræðilegra líkana: Lítil dreifni getur verið vísbending um að þú sért að lýsa handahófi villu eða hávaða í stað undirliggjandi tengsla í gögnum. Með þessari grein kennir wikiHow þér hvernig á að reikna dreifni.
Skref
Aðferð 1 af 2: Reiknið dreifni sýnis
Skrifaðu sýnisgagnasettið þitt. Í flestum tilvikum hafa tölfræðingar aðeins upplýsingar um úrtak, eða undirhóp íbúanna sem þeir eru að rannsaka. Til dæmis, í stað þess að gera almenna greiningu á „kostnaði allra bíla í Þýskalandi“, gæti tölfræðingur fundið kostnað við handahófsúrtak sem er nokkur þúsund bílar. Tölfræðingurinn getur notað þetta úrtak til að fá gott mat á bílakostnaði í Þýskalandi. Hins vegar er líklegra að það passi ekki nákvæmlega við raunverulegar tölur.
- Til dæmis: Þegar þú greindir fjölda muffins sem seldur er á dag á kaffihúsi, tókstu tilviljanakennd sex daga sýni og fékkst eftirfarandi niðurstöður: 38, 37, 36, 28, 18, 14, 12, 11, 10,7, 9,9. Þetta er sýnishorn, ekki íbúar, því þú hefur ekki gögn fyrir hvern dag sem verslunin er opin.
- Ef hvert Gögn stig í skipstjóra, vinsamlegast farðu í aðferðina hér að neðan.

Skrifaðu niður fráviksformúluna. Dreifni gagnasafns gefur til kynna dreifingarstig gagnapunktanna. Því nær sem dreifni er núll því nær eru gagnapunktarnir flokkaðir. Þegar unnið er með sýnishorn af gagnasettum, notaðu eftirfarandi formúlu til að reikna dreifni:- = /(n - 1)
- er dreifni. Afbrigði er alltaf reiknað í fermetra einingum.
- táknar gildi í gagnasettinu þínu.
- ∑, sem þýðir "summa", segir þér að reikna eftirfarandi breytur fyrir hvert gildi og bæta þeim síðan saman.
- x̅ er meðaltal sýnisins.
- n er fjöldi gagnapunkta.

Reiknið meðaltal sýnisins. Táknið x̅ eða „x-lárétt“ er notað til að gefa til kynna meðaltal sýnisins. Reiknið eins og meðaltalið: leggið saman alla gagnapunktana og deilið þeim með fjölda punkta.- Til dæmis: Fyrst skaltu bæta við gagnapunktana þína: 17 + 15 + 23 + 7 + 9 + 13 = 84
Deilið næst niðurstöðunni með fjölda gagnapunkta, í þessu tilfelli sex: 84 ÷ 6 = 14.
Dæmi meðaltal = x̅ = 14. - Þú getur hugsað um meðaltalið sem „miðpunkt“ gagnanna. Ef gögnin eru miðuð í kringum meðaltalið er dreifni lítil. Ef þeir dreifast langt frá meðaltali er dreifni mikil.
- Til dæmis: Fyrst skaltu bæta við gagnapunktana þína: 17 + 15 + 23 + 7 + 9 + 13 = 84

Dragðu meðaltalið frá hverjum gagnapunkti. Nú er kominn tími til að reikna - x̅, þar sem hver punktur í gagnasafninu þínu er. Hver niðurstaða gefur til kynna frávik frá meðaltali hvers samsvarandi punktar, eða til að setja það einfaldlega, fjarlægðina frá því að meðaltalinu.- Til dæmis:
- x̅ = 17 - 14 = 3
- x̅ = 15 - 14 = 1
- x̅ = 23 - 14 = 9
- x̅ = 7 - 14 = -7
- x̅ = 9 - 14 = -5
- x̅ = 13 - 14 = -1 - Það er mjög auðvelt að athuga útreikninga þína, vegna þess að niðurstöðurnar verða að hljóða upp á núll. jákvæðar niðurstöður (fjarlægð frá meðaltali í stærri tölur) eru eytt að fullu.
- Til dæmis:
Veldu allar niðurstöður. Eins og fram hefur komið hér að ofan er núverandi frávikslisti (- x̅) með summan núll.Það þýðir að „meðaltalsfrávikið“ verður líka alltaf núll og ekkert er hægt að segja um dreifingu gagnanna. Til að leysa þetta vandamál finnum við ferning hvers fráviks. Þökk sé því eru öll jákvæðar tölur, neikvæð gildi og jákvæð gildi hætta ekki lengur við hvert annað og gefa summuna núll.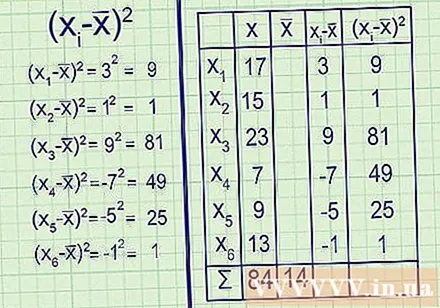
- Til dæmis:
(- x̅)
- x̅)
9 = 81
(-7) = 49
(-5) = 25
(-1) = 1 - Þú hefur nú (- x̅) fyrir hvern gagnapunkt í sýninu.
- Til dæmis:
Finndu summu ferningsgildanna. Nú er kominn tími til að reikna allan teljara formúlunnar: ∑. Stóri hringrásin, ∑, krefst þess að þú bætir við eftirfarandi þáttagildi fyrir hvert gildi. Þú hefur reiknað (- x̅) fyrir hvert gildi í úrtakinu, svo það eina sem þú þarft að gera er bara að bæta niðurstöðunum saman.
- Til dæmis: 9 + 1 + 81 + 49 + 25 + 1 = 166.
Deildu með n - 1, þar sem n er fjöldi gagnapunkta. Fyrir löngu, við útreikning á fráviki, voru tölfræðingar aðeins deilt með n. Sú skipting gefur þér meðaltal ferningsfráviksins, sem passar nákvæmlega við dreifni þess úrtaks. Hafðu samt í huga að úrtakið er aðeins mat á stærri þýði. Ef þú tekur annað slembiúrtak og gerir sama útreikning muntu fá aðra niðurstöðu. Þegar kemur að því að deila með n -1 í stað n gefur þér betra mat á dreifni stærri íbúa - sem þér þykir vænt um. Þessi leiðrétting er svo algeng að hún er nú viðurkennd skilgreining á afbrigði úrtaks.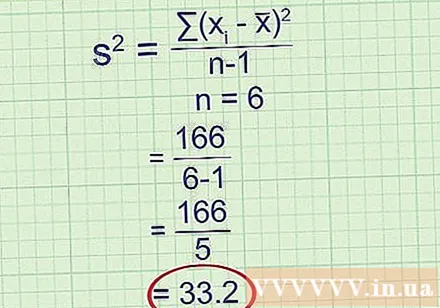
- Til dæmis: Það eru sex gagnapunktar í úrtakinu, svo n = 6.
Dæmi dreifni = 33,2
- Til dæmis: Það eru sex gagnapunktar í úrtakinu, svo n = 6.
Skilja dreifni og staðalfrávik. Athugið að þar sem kraftar eru í formúlunni er dreifni mæld í fermetri eininganna í upphaflegu gögnunum. Þetta er sjónrænt ruglingslegt. Í staðinn er oft staðalfrávikið mjög gagnlegt. En það þýðir ekkert að eyða neinni viðleitni, þar sem staðalfrávikið er ákvarðað af kvaðratrót dreifninnar. Þess vegna er frávikssniðið skrifað með skilmálum og staðalfrávik sýnis er.
- Til dæmis er staðalfrávik ofangreinds sýnis = s = √33,2 = 5,76.
Aðferð 2 af 2: Reiknið dreifni íbúa
Byrjar á aðalgagnasettinu. Hugtakið „íbúar“ er notað til að vísa til allra athugana sem máli skipta. Til dæmis, ef þú ert að rannsaka aldur íbúa Hanoi mun almenningur þinn fela í sér aldur allra einstaklinga sem búa í Hanoi. Venjulega myndirðu búa til töflureikni fyrir stórt gagnasafn eins og þetta, en hér er minna dæmi um gagnasett:
- Til dæmis: Í herbergi fiskabúrs eru nákvæmlega sex fiskabúr. Þessir sex tankar innihalda eftirfarandi fjölda fiska:
- Til dæmis: Í herbergi fiskabúrs eru nákvæmlega sex fiskabúr. Þessir sex tankar innihalda eftirfarandi fjölda fiska:
Skrifaðu formúluna fyrir heildarafbrigði. Þar sem þýðið inniheldur öll gögn sem við þurfum, þá gefur þessi formúla okkur nákvæmlega dreifni íbúanna. Til að greina það fráviksdreifinu (sem er aðeins mat) nota tölfræðingar aðrar breytur:
- σ = /n
- σ = afbrigðissýni. Þetta er venjulega ferkantaða pylsan. Dreifni er mæld í fermetra einingum.
- táknar þátt í gagnasettinu þínu.
- Stakurinn í ∑ er reiknaður fyrir hvert gildi og síðan bætt saman.
- μ er heildarmeðaltalið.
- n er fjöldi gagnapunkta í þýði.
Finndu meðaltal íbúa. Við greiningu á þýði táknar táknið μ („mu“) reikniaðaltalið. Til að finna meðaltalið skaltu leggja saman alla gagnapunktana og deila síðan með fjölda punkta.
- Þú getur hugsað um meina sem „meðaltal“ en vertu varkár, því orðið hefur margar stærðfræðilegar skilgreiningar.
- Til dæmis: meðalgildi = μ = = 10,5
Dragðu meðaltalið frá hverjum gagnapunkti. Gagnapunktar nær meðaltali hafa mun nær núlli. Endurtaktu frádráttarvandamálið fyrir alla gagnapunkta og þú munt líklega finna fyrir dreifingu gagnanna.
- Til dæmis:
- μ = 5 – 10,5 = -5,5
- μ = 5 – 10,5 = -5,5
- μ = 8 – 10,5 = -2,5
- μ = 12 - 10., = 1,5
- μ = 15 – 10,5 = 4,5
- μ = 18 – 10,5 = 7,5
- Til dæmis:
Square hvert skilti. Á þessum tímapunkti verða sumar niðurstöður sem fengust frá fyrra skrefi neikvæðar og aðrar jákvæðar.Ef þú sýnir gögnin á ísómorfri línu tákna þessi tvö atriði tölurnar til vinstri og hægri við meðaltalið. Þetta myndi ekki nýtast við útreikning á dreifni, þar sem þessir tveir hópar myndu hætta hvor öðrum. Í staðinn, veldu þá alla svo þeir séu allir jákvæðir.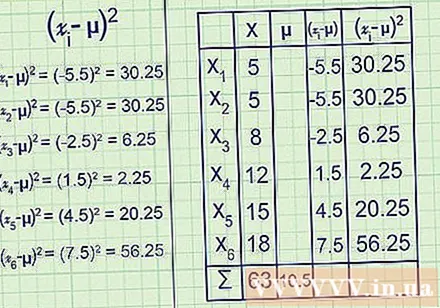
- Til dæmis:
(- μ) fyrir hvert gildi ég keyrir frá 1 til 6:
(-5,5) = 30,25
(-5,5) = 30,25
(-2,5) = 6,25
(1,5) = 2,25
(4,5) = 20,25
(7,5) = 56,25
- Til dæmis:
Finndu meðaltal niðurstaðna þinna. Þú hefur nú gildi fyrir hvern gagnapunkt, sem tengist (ekki beint) hversu langt í burtu þessi gagnapunktur er frá meðaltalinu. Meðaltal með því að leggja þau saman og deila með fjölda gilda sem þú hefur.
- Til dæmis:
Heildar dreifni = 24,25
- Til dæmis:
Hafðu samband við uppskrift. Ef þú ert ekki viss um hvernig þetta passar við formúluna sem lýst var í upphafi aðferðarinnar, skrifaðu allt vandamálið niður með höndunum og ekki stytta það: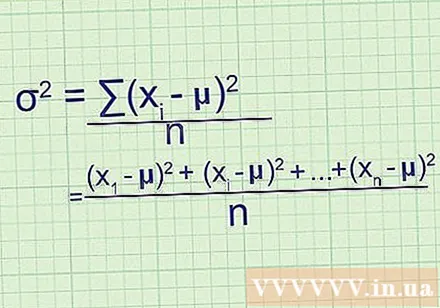
- Eftir að hafa fundið muninn frá meðaltali og ferningi færðu (- μ), (- μ) og svo framvegis þar til (- μ), hvar er síðasti gagnapunkturinn. í gagnasafninu.
- Til að finna meðaltal þessara gilda skaltu bæta þeim saman og deila með n: ((- μ) + (- μ) + ... + (- μ)) / n
- Eftir að þú hefur umritað teljara með sigmoid táknun hefurðu /n, formúluafbrigði.
Ráð
- Vegna þess að frávikið er erfitt að túlka er þetta gildi oft reiknað sem upphafspunktur fyrir að finna staðalfrávikið.
- Að nota „n-1“ í stað „n“ í nefnara er tækni sem kallast Bessel leiðrétting. Úrtakið er aðeins mat á heildar þýði og meðaltal sýnisins hefur ákveðna hlutdrægni til að passa við það mat. Þessi leiðrétting útrýma ofangreindri hlutdrægni. Það varðar þá staðreynd að þegar n - 1 gagnapunktar hafa verið taldir upp, síðasti liðurinn n var stöðugur, því aðeins tiltekin gildi voru notuð til að reikna meðaltal sýnisins (x̅) í dreififormúlunni.