Efni.

• Skref
• Ábendingar

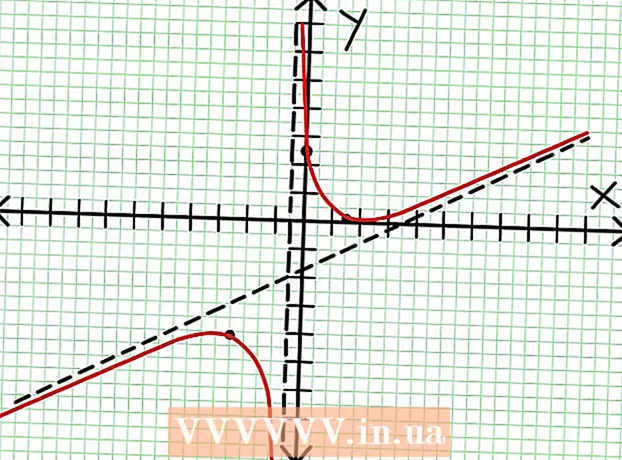
Rökfallið hefur formið y = N (x) / D (x), þar sem N og D eru margliða. Til að teikna slíka aðgerð nákvæmlega þarftu góða þekkingu á algebru, þar með talið mismunareikningum. Íhugaðu eftirfarandi dæmi: y = (2x - 6x + 5)/(4x + 2).

Skref

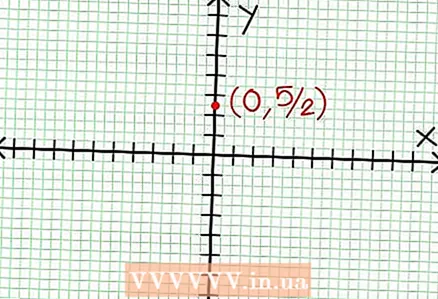1. 1 Finndu y-hlerun myndarinnar. Til að gera þetta skaltu skipta x = 0 í fallið og fá y = 5/2. Þannig hefur skeripunktur línuritsins með Y -ásnum hnit (0, 5/2).Settu þennan punkt á hnitaplanið.
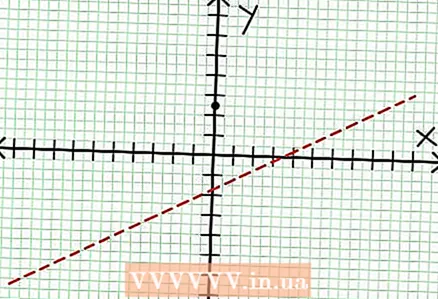2. 2 Finndu láréttu einkennin. Deildu teljara með nefnara (í dálki) til að ákvarða hegðun „y“ með gildum „x“ sem hafa tilhneigingu til óendanleika. Í okkar dæmi verður skiptingin y = (1/2)x - (7/4) + 17/(8x + 4). Fyrir stór jákvæð eða neikvæð gildi „x“ 17 / (8x + 4) hefur tilhneigingu til núlls og línuritið nálgast beina línu sem fallið gefur y = (1/2)x - (7/4). Notaðu punktalínuna og teiknaðu þessa aðgerð.
   • Ef stig teljarans er lægra en nefnari, þá er ekki hægt að deila tölunni með nefninum og einkennalausninni verður lýst með fallinu kl = 0.
   • Ef stig teljarans er jafnt stigi nefnara, þá er asymptote lárétt lína sem jafngildir hlutfalli stuðlanna við "x" í hæstu stigi.
   • Ef stig teljarans er 1 meira en gráður nefnara, þá er asymptote hallandi bein lína, halla hennar er jöfn hlutfalli stuðlanna við "x" í hæsta stig.
   • Ef stig teljarans er hærra en nefnara með 2, 3 osfrv., Þá fyrir stór gildi |NS| merkingu kl hafa tilhneigingu til óendanleika (jákvætt eða neikvætt) í formi fernings, rúmmetra eða annars stigs margliða. Í þessu tilviki er líklegast að þú þurfir ekki að byggja upp nákvæm línurit yfir fallið sem fæst með því að deila tölunni með nefninum.
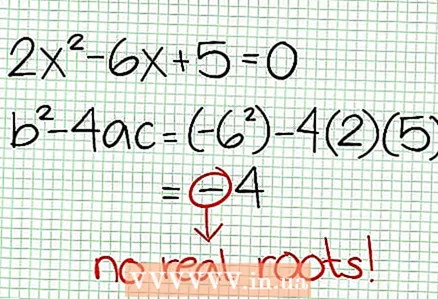3. 3 Finndu núll fallsins. Rökfall hefur núll þegar númer þess er núll, það er N (NS) = 0. Í dæminu okkar, 2x - 6x + 5 = 0. Mismunurinn á þessari fjórðu jöfnu: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Þar sem mismununarmaðurinn er neikvæður, þá er N (NS), og þess vegna F (NS) á sér engar raunverulegar rætur. Línurit skynsemis falls sker ekki X-ásinn. Ef fallið hefur núll (rætur), settu það þá á hnitaplanið.
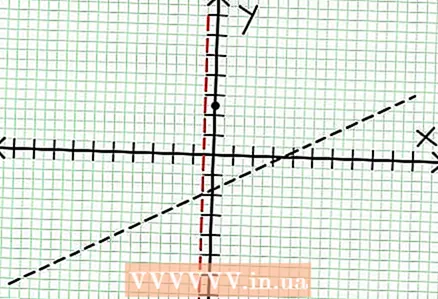4. 4 Finndu lóðréttu einkennin. Til að gera þetta, stilltu nefnara á núll. Í dæmi okkar, 4x + 2 = 0 og NS = -1/2. Teiknaðu lóðréttu asymptótuna með punktalínunni. Ef fyrir einhver verðmæti NS N (NS) = 0 og D (NS) = 0, þá er lóðrétt asymptote annaðhvort til eða er ekki til (þetta er sjaldgæft tilfelli, en betra er að muna það).
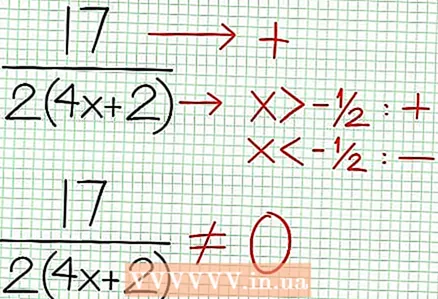5. 5 Horfðu á afganginn af teljara deilt með nefnara. Er það jákvætt, neikvætt eða núll? Í okkar dæmi er afgangurinn 17, sem er jákvætt. Nefnari 4x + 2 jákvæð til hægri við lóðréttu einkennalausu og neikvæð til vinstri við hana. Þetta þýðir að línurit skynsamlegra falla fyrir stór jákvæð gildi NS nálgast einkennin að ofan og fyrir stór neikvæð gildi NS - að neðan. Síðan 17 / (8x + 4) er aldrei jafnt og núll, þá mun línurit þessarar aðgerðar aldrei skerast í beina línu sem tilgreind er með fallinu kl = (1/2)NS - (7/4).
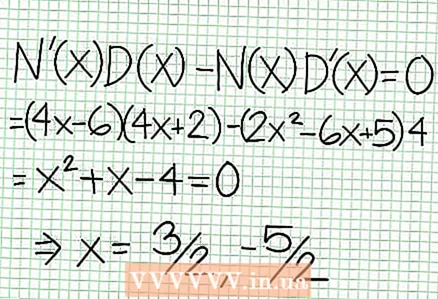6. 6 Finndu staðbundið extrema. Staðbundin extremum er til fyrir N '(x) D (x) - N (x) D ’(x) = 0. Í dæminu okkar er N ’(x) = 4x - 6 og D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Að leysa þessa jöfnu, þú finnur það x = 3/2 og x = -5/2. (Þetta eru ekki alveg nákvæm gildi, en þau henta í okkar tilfelli þegar ofur nákvæmni er ekki þörf.)
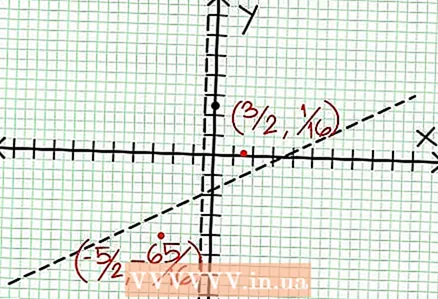7. 7 Finndu verðmæti kl fyrir hvert staðbundið extremum. Til að gera þetta skaltu skipta gildunum út NS inn í upphaflega skynsamlega virkni. Í dæminu okkar er f (3/2) = 1/16 og f (-5/2) = -65/16. Settu til hliðar punkta (3/2, 1/16) og (-5/2, -65/16) á hnitaplaninu. Þar sem útreikningarnir eru byggðir á áætluðum gildum (frá fyrra skrefi) eru lágmark og hámark sem finnast heldur ekki alveg rétt (en líklega mjög nálægt nákvæmum gildum). (Punkturinn (3/2, 1/16) er mjög nálægt staðbundnu lágmarki. Frá og með skrefi 3 vitum við það kl alltaf jákvætt fyrir NS> -1/2, og við fundum lítið gildi (1/16); þannig að villugildið er afar lítið í þessu tilfelli.)
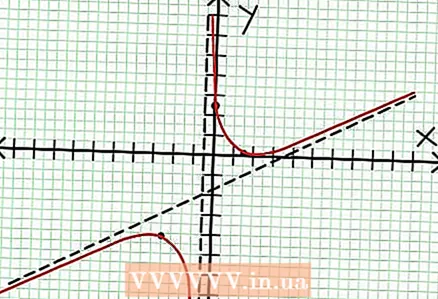8. 8 Tengdu punktana sem bíða og teygðu línuritið mjúklega að einkennalausum merkingum (ekki gleyma réttri stefnu línunnar sem nálgast einkennalausnir). Mundu að línuritið má ekki fara yfir X-ásinn (sjá skref 3). Línuritið sker ekki heldur við láréttu og lóðréttu einkennalausu merkin (sjá skref 5). Ekki breyta stefnu töflunnar nema á þeim öfgastöðum sem fundust í fyrra skrefi.

Ábendingar

• Ef þú hefur fylgt ofangreindum skrefum nákvæmlega í röð, þá er engin þörf á að reikna út síðari afleiður (eða svipað flókið magn) til að prófa lausn þína.
• Ef þú þarft ekki að reikna út magngildi geturðu skipt út fyrir staðbundið extrema með því að reikna út nokkur hnitapör (NS, kl) milli hvers pars einkennalausra. Þar að auki, ef þér er alveg sama hvernig lýst er aðferðinni, þá ekki vera hissa á því hvers vegna þú getur ekki fundið afleiðuna og leyst jöfnuna N '(x) D (x) - N (x) D ’(x) = 0.
• Í sumum tilfellum verður þú að vinna með margliða í hærri röð. Ef þú getur ekki fundið nákvæma lausn með stuðlunarstuðli, formúlum osfrv., Áætlaðu þá mögulegar lausnir með tölulegum aðferðum eins og aðferð Newtons.
• Í mjög sjaldgæfum tilfellum deila teller og nefnari sameiginlegum breytuþætti. Samkvæmt skrefunum sem lýst er mun þetta leiða til núlls og lóðréttrar asymptote á sama stað. Hins vegar er þetta ekki hægt og skýringin er ein af eftirfarandi:
  • Núll í N (NS) hefur meiri margföldun en núll í D (NS). Mynd F (NS) hefur tilhneigingu til núlls á þessum tímapunkti, en er ekki skilgreint þar. Tilgreindu þetta með því að teikna hring um punktinn.
  • Núll í N (NS) og núll í D (NS) hafa sama margföldun. Myndritið nálgast einhvern punkt sem er núlllaus við þetta gildi NSen ekki skilgreint þar. Tilgreindu þetta með því að teikna hring um punktinn.
  • Núll í N (NS) hefur lægri margföldun en núll í D (NS). Það er lóðrétt asymptote hér.