Höfundur:
Marcus Baldwin
Sköpunardag:
16 Júní 2021
Uppfærsludagsetning:
1 Júlí 2024
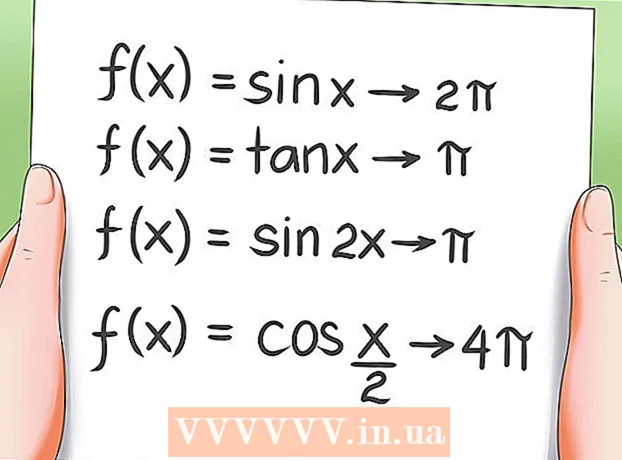
Efni.
Þríhyrningafræðileg jöfnu inniheldur eina eða fleiri þríhyrningafræðilega fall breytunnar „x“ (eða aðra breytu). Að leysa þríhyrningafræðilega jöfnu er að finna slíkt gildi „x“ sem fullnægir fallinu (s) og jöfnunni í heild.
- Lausnir á þríhyrningsfræðilegum jöfnum eru gefnar upp í gráðum eða radíönum. Dæmi:
x = π / 3; x = 5π / 6; x = 3π / 2; x = 45 gráður; x = 37,12 gráður; x = 178,37 gráður.
- Athugið: Gildi þríhyrningafræðilegra falla frá hornum, gefið upp í radíanum og frá hornum, gefið upp í gráðum, eru jöfn. Þríhyrningshringur með radíus sem er jafngildur einum er notaður til að lýsa þríhyrningafræðilegum aðgerðum, svo og til að athuga hvort lausnin á grundvallaratriðum þrívíddarjöfnna og misréttis sé rétt.
- Dæmi um þríhyrningafræðilegar jöfnur:
- sin x + sin 2x = 1/2; tg x + ctg x = 1,732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.
- Þríhyrningshringur með radíus einn (einingarhringur).
- Það er hringur með radíus sem er jafn einn og miðpunktur við punkt O. Einingarhringurinn lýsir 4 grundvallaratriðum þríhyrningafræðilegum aðgerðum breytunnar „x“, þar sem „x“ er hornið sem er mælt frá jákvæðri átt X -ássins rangsælis.
- Ef „x“ er einhver horn á einingarhringnum, þá:
- Lárétti ásinn OAx skilgreinir fallið F (x) = cos x.
- Lóðrétti ásinn OBy skilgreinir fallið F (x) = sin x.
- Lóðrétti ásinn AT skilgreinir fallið F (x) = tan x.
- Lárétti ásinn BU skilgreinir fallið F (x) = ctg x.
- Einingarhringurinn er einnig notaður til að leysa grundvallar þríhyrningafræðilegar jöfnur og misrétti (litið er til mismunandi staða „x“ á honum).
Skref
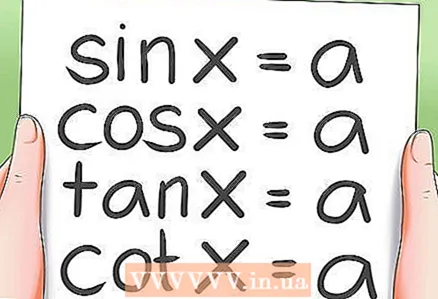 1 Hugmyndin um að leysa þrívíddarjöfnur.
1 Hugmyndin um að leysa þrívíddarjöfnur.- Til að leysa þríhyrningsjöfnu skal breyta henni í eina eða fleiri grundvallar þrívíddarjöfnur. Að leysa þríhyrningjafræðilega jöfnu kemur að lokum niður á að leysa fjórar grundvallar þrívíddarjöfnur.
 2 Að leysa grundvallar þríhyrningafræðilegar jöfnur.
2 Að leysa grundvallar þríhyrningafræðilegar jöfnur.- Það eru til 4 gerðir af grundvallar þríhyrningafræðilegum jöfnum:
- synd x = a; cos x = a
- tg x = a; ctg x = a
- Að leysa grundvallar þrívíddarjöfnur felur í sér að skoða mismunandi x stöður einingarhringsins og nota umbreytitöflu (eða reiknivél).
- Dæmi 1.sin x = 0,866. Með því að nota umbreytitöflu (eða reiknivél) færðu svarið: x = π / 3. Einingarhringurinn gefur annað svar: 2π / 3. Mundu: allar þríhyrningafræðilegar aðgerðir eru reglubundnar, það er að segja gildi þeirra eru endurtekin. Til dæmis er tíðni sin x og cos x 2πn og tíðni tg x og ctg x er πn. Þess vegna er svarið skrifað þannig:
- x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
- Dæmi 2.kos x = -1/2. Með því að nota umbreytitöflu (eða reiknivél) færðu svarið: x = 2π / 3. Einingarhringurinn gefur annað svar: -2π / 3.
- x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
- Dæmi 3.tg (x - π / 4) = 0.
- Svar: x = π / 4 + πn.
- Dæmi 4. ctg 2x = 1.732.
- Svar: x = π / 12 + πn.
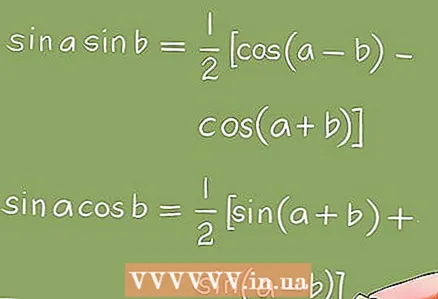 3 Umbreytingar sem notaðar eru til að leysa þrívíddarjöfnur.
3 Umbreytingar sem notaðar eru til að leysa þrívíddarjöfnur.- Til að umbreyta þríhyrningsjöfnum eru algebrubreytingar (þáttun, fækkun einsleitra hugtaka osfrv.) Og þríhyrnifræðileg auðkenni notuð.
- Dæmi 5. Með þríhyrningafræðilegum auðkenni breytist jöfnan sin x + sin 2x + sin 3x = 0 í jöfnuna 4cos x * sin (3x / 2) * cos (x / 2) = 0. Þannig þarftu að leysa eftirfarandi grundvallar þríhyrningafræðilegar jöfnur: cos x = 0; sin (3x / 2) = 0; cos (x / 2) = 0.
 4 Að finna horn frá þekktum gildum virka.
4 Að finna horn frá þekktum gildum virka.- Áður en þú lærir aðferðir til að leysa þrívíddarjöfnur þarftu að læra hvernig á að finna horn frá þekktum gildum falla. Þetta er hægt að gera með því að nota umbreytitöflu eða reiknivél.
- Dæmi: cos x = 0,732. Reiknivélin mun gefa svarið x = 42,95 gráður. Einingarhringurinn mun gefa fleiri horn en kósínusinn er einnig 0,732.
 5 Settu lausnina til hliðar á einingarhringinn.
5 Settu lausnina til hliðar á einingarhringinn.- Þú getur frestað lausnum á þríhyrningafræðilegu jöfnunni á einingarhringnum. Lausnir þrívíddarjöfnunnar á einingarhringnum eru hornpunktar venjulegs marghyrnings.
- Dæmi: lausnirnar x = π / 3 + πn / 2 á einingarhringnum eru hornpunktar fernings.
- Dæmi: lausnirnar x = π / 4 + πn / 3 á einingarhringnum tákna hornpunkta venjulegs sexhyrnings.
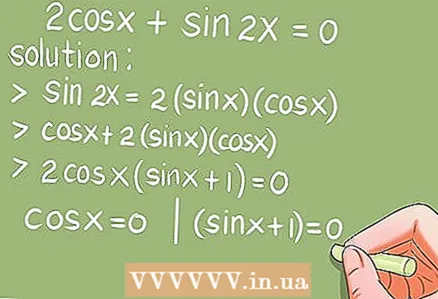 6 Aðferðir til að leysa þrívíddarjöfnur.
6 Aðferðir til að leysa þrívíddarjöfnur.- Ef tiltekin þrígjafna inniheldur aðeins eitt þrígildi skal leysa þá jöfnu sem grunntrígjafna.Ef tiltekin jöfnu inniheldur tvær eða fleiri þríhyrningafræðilegar aðgerðir, þá eru til tvær aðferðir til að leysa slíka jöfnu (fer eftir möguleikum á umbreytingu hennar).
- Aðferð 1.
- Breytið þessari jöfnu í jöfnu á forminu: f (x) * g (x) * h (x) = 0, þar sem f (x), g (x), h (x) eru grundvallar þrívíddarjöfnur.
- Dæmi 6.2cos x + sin 2x = 0. (0 x 2π)
- Lausn. Með því að nota tvöfalda hornformúlu sin 2x = 2 * sin x * cos x, skiptu út sin 2x.
- 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Leysið nú grundvallar þríhyrningafræðilega jöfnurnar: cos x = 0 og (sin x + 1) = 0.
- Dæmi 7. cos x + cos 2x + cos 3x = 0. (0 x 2π)
- Lausn: Með því að nota þríhyrningafræðilega auðkenni, umbreytið þessari jöfnu í jöfnu á forminu: cos 2x (2cos x + 1) = 0. Leysið nú grundvallar þríhyrningafræðilega jöfnurnar: cos 2x = 0 og (2cos x + 1) = 0.
- Dæmi 8.sin x - sin 3x = cos 2x. (0 x 2π)
- Lausn: Með því að nota þríhyrningafræðilega auðkenni, umbreytið þessari jöfnu í jöfnu á forminu: -cos 2x * (2sin x + 1) = 0. Leysið nú tvær þríhyrningjafræðilegar jöfnur: cos 2x = 0 og (2sin x + 1) = 0.
- Aðferð 2.
- Breytið tilgreindum þríhyrningsjöfnu í jöfnu sem inniheldur aðeins eina þríhyrnifræðilega virkni. Settu síðan þessa þríhyrnifræðilega virkni í staðinn fyrir einhverja óþekkta, til dæmis t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t osfrv.).
- Dæmi 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
- Lausn. Í þessari jöfnu skal skipta út (cos ^ 2 x) fyrir (1 - sin ^ 2 x) (eftir sjálfsmynd). Breytta jöfnan er:
- 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Skiptu um sin x með t. Jafnan lítur nú svona út: 5t ^ 2 - 4t - 9 = 0. Þetta er ferningsjöfnu með tveimur rótum: t1 = -1 og t2 = 9/5. Önnur rótin t2 uppfyllir ekki gildissvið fallsins (-1 sin x 1). Nú skaltu ákveða: t = sin x = -1; x = 3π / 2.
- Dæmi 10. tg x + 2 tg ^ 2 x = ctg x + 2
- Lausn. Skipta út tg x fyrir t. Endurskrifaðu upphaflegu jöfnuna þannig: (2t + 1) (t ^ 2 - 1) = 0. Finndu nú t og finndu síðan x fyrir t = tg x.
- Ef tiltekin þrígjafna inniheldur aðeins eitt þrígildi skal leysa þá jöfnu sem grunntrígjafna.Ef tiltekin jöfnu inniheldur tvær eða fleiri þríhyrningafræðilegar aðgerðir, þá eru til tvær aðferðir til að leysa slíka jöfnu (fer eftir möguleikum á umbreytingu hennar).
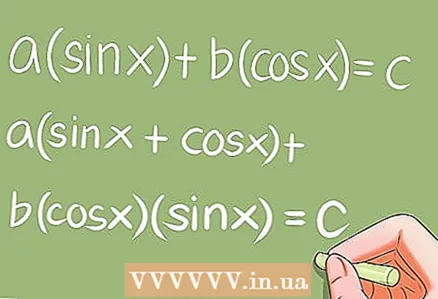 7 Sérstakar þríhyrningafræðilegar jöfnur.
7 Sérstakar þríhyrningafræðilegar jöfnur.- Það eru nokkrar sérstakar þríhyrningafræðilegar jöfnur sem krefjast sérstakra umbreytinga. Dæmi:
- a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
- a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
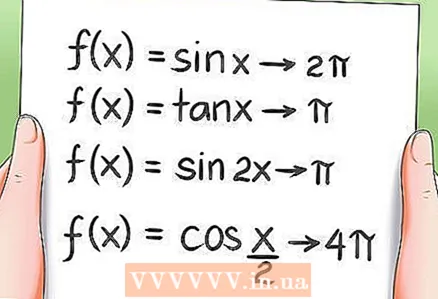 8 Tíðni þríhyrningafræðilegra aðgerða.
8 Tíðni þríhyrningafræðilegra aðgerða.- Eins og áður hefur komið fram eru allar þríhyrningafræðilegar aðgerðir reglubundnar, það er að segja gildi þeirra eru endurtekin eftir ákveðið tímabil. Dæmi:
- Tímabil fallsins f (x) = sin x er 2π.
- Tímabil fallsins f (x) = tan x er jafnt og π.
- Tímabil fallsins f (x) = sin 2x er π.
- Tímabil fallsins f (x) = cos (x / 2) er 4π.
- Ef tímabilið er tilgreint í vandamálinu, reiknaðu gildi "x" innan þessa tímabils.
- Athugið: Að leysa þrívíddarjöfnur er ekki auðvelt verk og leiðir oft til villna. Svo athugaðu svör þín vandlega. Til að gera þetta getur þú notað línurit reiknivél til að teikna uppgefna jöfnu R (x) = 0. Í slíkum tilfellum verða lausnir settar fram sem aukastafabrot (það er að π er skipt út fyrir 3.14).
- Eins og áður hefur komið fram eru allar þríhyrningafræðilegar aðgerðir reglubundnar, það er að segja gildi þeirra eru endurtekin eftir ákveðið tímabil. Dæmi: