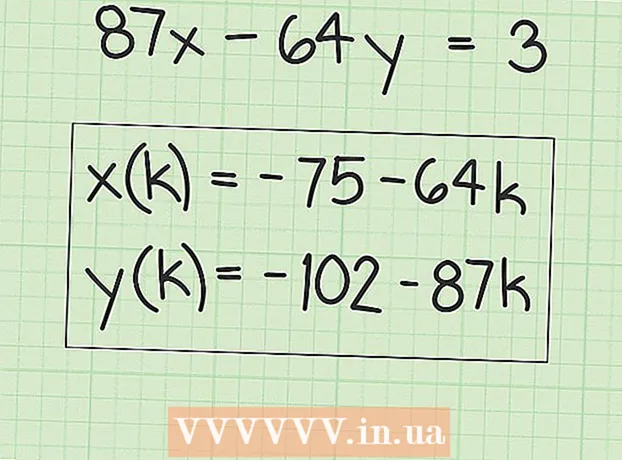
Efni.

• Skref
• 1. hluti af 4: Hvernig á að skrifa jöfnu
• Hluti 2 af 4: Hvernig á að skrifa reiknirit Euclides
• Hluti 3 af 4: Hvernig á að finna lausn með því að nota reiknirit Euclid
• Hluti 4 af 4: Finndu óendanlega aðrar lausnir

Til að leysa línulega Diophantine jöfnu þarftu að finna gildi breytanna "x" og "y", sem eru heiltölur. Heiltala lausn er flóknari en venjulega og krefst sérstakrar aðgerðar. Fyrst þarftu að reikna út stærsta sameiginlega skiptinguna (GCD) stuðlanna og finna síðan lausn. Þegar þú hefur fundið eina heiltölu lausn á línulegri jöfnu geturðu notað einfalt mynstur til að finna óendanlegan fjölda annarra lausna.

Skref

1. hluti af 4: Hvernig á að skrifa jöfnu

1. 1 Skrifaðu jöfnuna niður á venjulegu formi. Línuleg jöfnu er jöfnu þar sem veldisstærðir breytanna fara ekki yfir 1. Til að leysa slíka línulega jöfnu, skrifaðu hana fyrst á staðlað form. Staðlað form línulegrar jöfnu lítur svona út: ${ displaystyle Ax + By = C}$, hvar ${ displaystyle A, B}$ og ${ displaystyle C}$ - heilar tölur.
   • Ef jöfnan er gefin í öðru formi skaltu koma henni á staðlað form með grunn algebrískum aðgerðum. Til dæmis, miðað við jöfnuna ${ displaystyle 23x + 4y -7x = -3y + 15}$... Gefðu svipuð hugtök og skrifaðu jöfnuna svona: ${ displaystyle 16x + 7y = 15}$.
2. 2 Einfaldaðu jöfnuna (ef mögulegt er). Þegar þú skrifar jöfnuna á stöðluðu formi, horfðu á stuðlana ${ displaystyle A, B}$ og ${ displaystyle C}$... Ef þessar líkur eru með GCD skaltu deila öllum þremur líkunum með því. Lausnin á svona einfaldaðri jöfnu verður einnig lausnin á upprunalegu jöfnunni.
   • Til dæmis, ef allir þrír stuðlarnir eru jafnir, deila þeim með að minnsta kosti 2. Til dæmis:
     • ${ displaystyle 42x + 36y = 48}$ (allir meðlimir deila með 2)
     • ${ displaystyle 21x + 18y = 24}$ (nú eru allir meðlimir deilanlegir með 3)
     • ${ displaystyle 7x + 6y = 8}$ (ekki er hægt að einfalda þessa jöfnu lengur)
3. 3 Athugaðu hvort hægt sé að leysa jöfnuna. Í sumum tilfellum geturðu strax fullyrt að jöfnan hefur engar lausnir. Ef stuðullinn "C" er ekki deilanlegur með GCD stuðlanna "A" og "B" hefur jöfnan engar lausnir.
   • Til dæmis ef báðir stuðlar ${ displaystyle A}$ og ${ displaystyle B}$ eru jöfn, þá er stuðullinn ${ displaystyle C}$ hlýtur að vera jafnt. En ef ${ displaystyle C}$ skrýtið, þá er engin lausn.
     • Jafnan ${ displaystyle 2x + 4y = 21}$ engar heiltölulausnir.
     • Jafnan ${ displaystyle 5x + 10y = 17}$ það eru engar heiltölulausnir þar sem vinstri hlið jöfnunnar er deilanleg með 5 og hægri hliðin ekki.

Hluti 2 af 4: Hvernig á að skrifa reiknirit Euclides

1. 1 Skilja reiknirit Euclides. Það er röð endurtekinna skiptinga þar sem fyrri afgangurinn er notaður sem næsti skiptir. Síðasti deilirinn sem deilir tölunum óaðskiljanlega er stærsti sameiginlegi deilirinn (GCD) af tölunum tveimur.
   • Til dæmis, við skulum finna GCD númeranna 272 og 36 með því að nota reiknirit Euclid:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Deildu stærri tölunni (272) með þeim smærri (36) og gaum að afganginum (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - deila fyrri deilunni (36) með fyrri afganginum (20). Takið eftir nýju leifinni (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - deila fyrri deilunni (20) með fyrri afganginum (16). Takið eftir nýju leifinni (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Deildu fyrri deilunni (16) með fyrri afganginum (4). Þar sem afgangurinn er 0 getum við sagt að 4 sé GCD upphaflegu tveggja tölanna 272 og 36.
2. 2 Notaðu reiknirit Euclid til stuðlanna "A" og "B". Þegar þú skrifar línulegu jöfnuna á stöðluðu formi, ákvarðuðu stuðlana "A" og "B" og notaðu síðan reiknirit Euclides til að finna GCD. Til dæmis gefið línulega jöfnu ${ displaystyle 87x-64y = 3}$.
   • Hér er reiknirit Euclides fyrir stuðla A = 87 og B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Finndu Greatest Common Factor (GCD). Þar sem síðasti deilirinn var 1 eru GCD 87 og 64 1. Þannig eru 87 og 64 frumtölur miðað við hvert annað.
4. 4 Greindu niðurstöðuna. Þegar þú finnur gcd stuðlana ${ displaystyle A}$ og ${ displaystyle B}$, berðu það saman við stuðulinn ${ displaystyle C}$ upphaflega jöfnuna. Ef ${ displaystyle C}$ deilanlegt með gcd ${ displaystyle A}$ og ${ displaystyle B}$, jöfnan er með heiltölu lausn; annars hefur jöfnan engar lausnir.
   • Til dæmis jöfnuna ${ displaystyle 87x-64y = 3}$ er hægt að leysa vegna þess að 3 er deilanlegt með 1 (gcd = 1).
   • Segjum til dæmis að GCD = 5. 3 er ekki jafnt deilanlegt með 5, þannig að þessi jöfnu hefur engar heiltölulausnir.
   • Eins og sýnt er hér að neðan, ef jöfnu hefur eina heiltölu lausn, hefur hún einnig óendanlega fjölda annarra heiltölu lausna.

Hluti 3 af 4: Hvernig á að finna lausn með því að nota reiknirit Euclid

1. 1 Númeraðu skrefin til að reikna út GCD. Til að finna lausnina á línulegri jöfnu þarftu að nota Euclidean reikniritið sem grundvöll fyrir skiptingar- og einföldunarferlið.
   • Byrjaðu á því að númera skrefin til að reikna út GCD. Útreikningsferlið lítur svona út:
     • ${ displaystyle { text {Step 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Step 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Step 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Step 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Step 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Step 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Step 7}}: 2 = (2 * 1) +0}$
2. 2 Gefðu gaum að síðasta skrefinu, þar sem eftir er. Endurskrifaðu jöfnuna fyrir þetta skref til að einangra afganginn.
   • Í dæminu okkar er síðasta skrefið með afganginn skref 6. Afgangurinn er 1. Skrifaðu jöfnu í skrefi 6 þannig:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Einangrað afganginn af fyrra skrefi. Þetta ferli er skref-fyrir-skref „fara upp“. Í hvert skipti sem þú einangrar afganginn í jöfnunni í fyrra skrefi.
   • Einangrað afganginn af jöfnunni í þrepi 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ eða ${ displaystyle 2 = 5-3}$
4. 4 Skipta um og einfalda. Taktu eftir því að jöfnan í skrefi 6 inniheldur töluna 2 og í jöfnunni í skrefi 5 er talan 2 einangruð. Svo í staðinn fyrir „2“ í jöfnunni í skrefi 6 skaltu skipta um tjáningu í skrefi 5:
   • ${ displaystyle 1 = 3-2}$ (jöfnu í þrepi 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (í stað 2 var tjáningu skipt út)
   • ${ displaystyle 1 = 3-5 + 3}$ (opnað sviga)
   • ${ displaystyle 1 = 2 (3) -5}$ (einfaldað)
5. 5 Endurtaktu skiptingar- og einföldunarferlið. Endurtaktu lýst ferli og farðu í gegnum Euklidíska reikniritið í öfugri röð. Í hvert skipti sem þú munt endurskrifa jöfnuna frá fyrra skrefi og tengja hana við síðustu jöfnu sem þú færð.
   • Síðasta skrefið sem við skoðuðum var skref 5. Svo farðu í skref 4 og einangraðu afganginn í jöfnunni fyrir það skref:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Settu þessa setningu í stað „3“ í síðustu jöfnu:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Haltu áfram með skiptingar- og einföldunarferlið. Þetta ferli verður endurtekið þar til þú nærð upphafsþrepi Evklíðs reikniritsins. Markmið ferlisins er að skrifa jöfnuna með stuðlunum 87 og 64 í upphaflegu jöfnunni sem á að leysa. Í dæminu okkar:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (skipti um tjáningu frá þrepi 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (skipti um tjáningu frá skrefi 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (skipti um tjáningu frá skrefi 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Endurskrifaðu jöfnuna sem myndast í samræmi við upphaflegu stuðlana. Þegar þú snýrð aftur að fyrsta þrepi reikningsrannsóknarinnar í Euclidean muntu sjá að jöfnan sem myndast inniheldur tvær stuðlar upprunalegu jöfnunnar. Endurskrifaðu jöfnuna þannig að röð hugtaka hennar passi við stuðla upphaflegu jöfnunnar.
   • Í dæminu okkar, upphaflega jöfnuna ${ displaystyle 87x-64y = 3}$... Þess vegna skaltu endurskrifa jöfnuna sem myndast þannig að stuðlarnir séu í samræmi.Taktu sérstaklega eftir stuðlinum "64". Í upprunalegu jöfnunni er þessi stuðull neikvæður og í reikniritum Evklídíu er hann jákvæður. Þess vegna verður að gera þáttinn 34 neikvæðan. Endanleg jöfnu verður skrifuð svona:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Notaðu viðeigandi margfaldara til að finna lausn. Athugið að í dæminu okkar er GCD = 1, þannig að endanleg jöfnu er 1. En upphafleg jöfnu (87x-64y) er 3. Þess vegna verður að margfalda öll hugtök í loka jöfnunni með 3 til að fá lausnina:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Skrifaðu heiltölu lausnina á jöfnuna. Tölurnar sem eru margfaldaðar með stuðlum upphaflegu jöfnunnar eru lausnirnar á þeirri jöfnu.
   • Í dæminu okkar, skrifaðu lausnina sem hnitapar: ${ displaystyle (x, y) = ( - 75, -102)}$.

Hluti 4 af 4: Finndu óendanlega aðrar lausnir

1. 1 Gerðu þér grein fyrir því að það eru óendanlega margar lausnir. Ef línuleg jöfnu hefur eina heiltölu lausn, þá verður hún að hafa óendanlega margar heiltölu lausnir. Hér er fljótleg sönnun (í algebrískri mynd):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (ef þú bætir „B“ við „x“ og dregur „A“ frá „y“, mun gildi upphaflegu jöfnunnar ekki breytast)
2. 2 Skráðu upphaflegu x- og y -gildin. Sniðmátið til að reikna út næstu (óendanlega) lausnir byrjar með eina lausninni sem þú hefur þegar fundið.
   • Í okkar dæmi er lausnin par af hnitum ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Bættu „B“ stuðlinum við „x“ gildið. Gerðu þetta til að finna nýja x gildið.
   • Í dæminu okkar, x = -75 og B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Þannig er nýja gildið „x“: x = -139.
4. 4 Dragðu „A“ þáttinn frá „y“ gildinu. Þannig að gildi upphaflegu jöfnunnar breytist ekki, þegar þú bætir einni tölu við „x“ þarftu að draga aðra tölu frá „y“.
   • Í dæminu okkar, y = -102 og A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Þannig er nýja gildið fyrir „y“: y = -189.
   • Nýja hnitaparið verður skrifað svona: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Athugaðu lausnina. Til að sannreyna að nýja hnitaparið sé lausn á upprunalegu jöfnunni skaltu stinga gildunum í jöfnuna.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Þar sem jafnrétti er fullnægt er ákvörðunin rétt.
6. 6 Skrifaðu niður orðatiltæki til að finna margar lausnir. "X" gildin jafngilda upprunalegu lausninni auk margfeldis af "B" stuðlinum. Þetta er hægt að skrifa sem eftirfarandi tjáningu:
   • x (k) = x + k (B), þar sem „x (k)“ er mengi „x“ gildis og „x“ er upphaflega (fyrsta) gildi „x“ sem þú fannst.
     • Í dæminu okkar:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), þar sem y (k) er mengi y gildanna og y er upphaflega (fyrsta) y gildið sem þú fannst.
     • Í dæminu okkar:
     • ${ displaystyle y (k) = - 102-87k}$