Efni.

• Skref
• Aðferð 1 af 4: Reikna fylgnistuðulinn handvirkt
• Aðferð 2 af 4: Notkun reiknivéla á netinu til að reikna fylgnistuðulinn
• Aðferð 3 af 4: Notkun grafreiknivél
• Aðferð 4 af 4: Að útskýra grunnhugtök
• Ábendingar
• Viðvaranir

Fylgistuðullinn (eða línuleg fylgnistuðull) er táknaður sem „r“ (í sjaldgæfum tilfellum sem „ρ“) og einkennir línulega fylgni (það er sambandið sem er gefið með einhverju gildi og stefnu) tveggja eða fleiri breytna. Gildi stuðilsins er á milli -1 og +1, það er að fylgnin getur verið bæði jákvæð og neikvæð. Ef fylgnistuðullinn er -1, þá er fullkomin neikvæð fylgni; ef fylgnistuðullinn er +1, þá er fullkomin jákvæð fylgni. Annars er jákvæð fylgni milli breytanna tveggja, neikvæð fylgni eða engin fylgni. Hægt er að reikna fylgnistuðulinn handvirkt, með ókeypis reiknivélum á netinu eða með góðum línuritareikni.

Skref

Aðferð 1 af 4: Reikna fylgnistuðulinn handvirkt

1. 1 Safna gögnum. Áður en þú byrjar að reikna fylgnistuðulinn skaltu rannsaka þessi talapör. Betra að skrifa þau niður í töflu sem hægt er að raða lóðrétt eða lárétt. Merktu hverja röð eða dálk með „x“ og „y“.
   • Til dæmis, gefið fjögur pör af gildum (tölum) breytanna „x“ og „y“. Þú getur búið til eftirfarandi töflu:
     • x || y
     • 1 || 1
     • 2 || 3
     • 4 || 5
     • 5 || 7
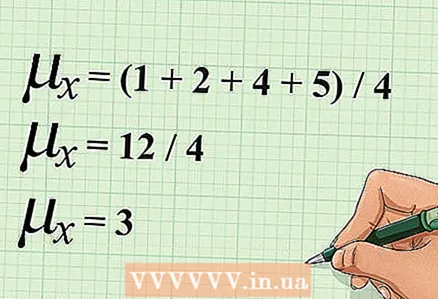2. 2 Reiknaðu reikningsmeðaltalið "x". Til að gera þetta skaltu leggja saman öll x -gildin og deila niðurstöðunni með fjölda gilda.
   • Í dæminu okkar eru fjögur gildi fyrir breytuna „x“. Til að reikna reikna meðaltalið "x", bætið við þessum gildum og deilið síðan summan með 4. Útreikningarnir eru skrifaðir sem hér segir:
   • ${ displaystyle mu _ {x} = (1 + 2 + 4 + 5) / 4}$
   • ${ displaystyle mu _ {x} = 12/4}$
   • ${ displaystyle mu _ {x} = 3}$
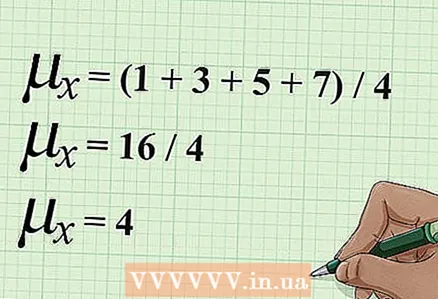3. 3 Finndu reikningsmeðaltalið „y“. Til að gera þetta skaltu fylgja sömu skrefunum, það er að segja að setja saman öll y -gildin og deila síðan summanum með fjölda gilda.
   • Í dæminu okkar eru gefin fjögur gildi breytunnar „y“. Bættu þessum gildum við og deildu síðan summan með 4. Útreikningarnir verða skrifaðir sem hér segir:
   • ${ displaystyle mu _ {y} = (1 + 3 + 5 + 7) / 4}$
   • ${ displaystyle mu _ {y} = 16/4}$
   • ${ displaystyle mu _ {y} = 4}$
4. 4 Reiknaðu staðalfrávikið "x". Eftir að hafa reiknað út meðaltölin „x“ og „y“ skaltu finna staðalfrávik þessara breytna. Staðalfrávikið er reiknað út með eftirfarandi formúlu:
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {n-1}} Sigma (x- mu _ {x}) ^ {2}}}}$
   • Í dæminu okkar verða útreikningarnir skrifaðir svona:
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {4-1}} * ((1-3) ^ {2} + (2-3) ^ {2} + ( 4-3) ^ {2} + (5-3) ^ {2})}}}}$
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {3}} * (4 + 1 + 1 + 4)}}}}$
   • ${ displaystyle sigma _ {x} = { sqrt {{ frac {1} {3}} * (10)}}}$
   • ${ displaystyle sigma _ {x} = { sqrt { frac {10} {3}}}}$
   • ${ displaystyle sigma _ {x} = 1.83}$
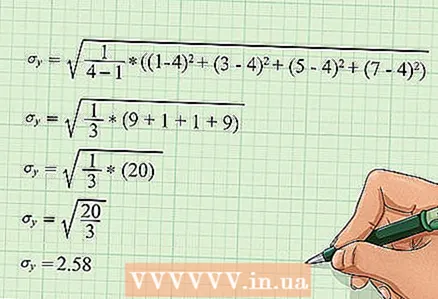5. 5 Reiknaðu staðalfrávikið „y“. Fylgdu skrefunum sem lýst var í fyrra skrefi. Notaðu sömu formúlu en settu inn y -gildin.
   • Í dæminu okkar verða útreikningarnir skrifaðir svona:
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {4-1}} * ((1-4) ^ {2} + (3-4) ^ {2} + ( 5-4) ^ {2} + (7-4) ^ {2})}}}}$
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {3}} * (9 + 1 + 1 + 9)}}}}$
   • ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {3}} * (20)}}}$
   • ${ displaystyle sigma _ {y} = { sqrt { frac {20} {3}}}}$
   • ${ displaystyle sigma _ {y} = 2,58}$
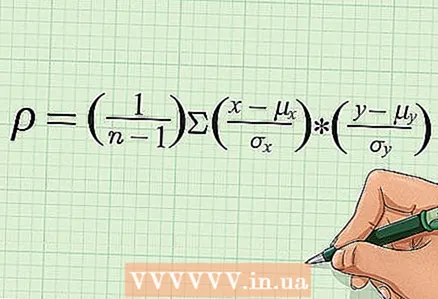6. 6 Skrifaðu niður grunnformúluna til að reikna út fylgnistuðulinn. Þessi formúla inniheldur meðalgildi, staðalfrávik og fjölda (n) af tölupörum beggja breytanna. Fylgistuðullinn er táknaður sem „r“ (í sjaldgæfum tilfellum sem „ρ“). Þessi grein notar formúlu til að reikna út Pearson fylgistuðulinn.
   • ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } hægri) * vinstri ({ frac {y- mu _ {y}} { sigma _ {y}}} hægri)}$
   • Hér og í öðrum heimildum er hægt að tákna magn á mismunandi hátt. Til dæmis innihalda sumar formúlur „ρ“ og „σ“ en aðrar innihalda „r“ og „s“. Sumar kennslubækur gefa mismunandi formúlur, en þær eru stærðfræðilegar hliðstæður við ofangreinda formúlu.
7. 7 Reiknaðu fylgnistuðulinn. Þú hefur reiknað út meðaltal og staðalfrávik beggja breytanna, svo þú getur notað formúluna til að reikna fylgnistuðulinn. Mundu að „n“ er fjöldi verðgildispara fyrir báðar breyturnar. Önnur gildi hafa verið reiknuð út fyrr.
   • Í dæminu okkar verða útreikningarnir skrifaðir svona:
   • ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } hægri) * vinstri ({ frac {y- mu _ {y}} { sigma _ {y}}} hægri)}$
   • ${ displaystyle rho = left ({ frac {1} {3}} right) *}$[${ displaystyle left ({ frac {1-3} {1.83}} right) * left ({ frac {1-4} {2.58}} right) + left ({ frac {2 -3} {1.83}} hægri) * vinstri ({ frac {3-4} {2.58}} hægri)}$
        ${ displaystyle + left ({ frac {4-3} {1.83}} right) * left ({ frac {5-4} {2.58}} right) + left ({ frac { 5-3} {1.83}} hægri) * vinstri ({ frac {7-4} {2.58}} hægri)}$]
   • ${ displaystyle rho = left ({ frac {1} {3}} right) * left ({ frac {6 + 1 + 1 + 6} {4.721}} right)}$
   • ${ displaystyle rho = left ({ frac {1} {3}} right) * 2.965}$
   • ${ displaystyle rho = left ({ frac {2,965} {3}} right)}$
   • ${ displaystyle rho = 0.988}$
8. 8 Greindu niðurstöðuna. Í dæminu okkar er fylgnistuðullinn 0,988. Þetta gildi einkennir á einhvern hátt tiltekið sett af tölustöfum. Gefðu gaum að merki og stærð verðmætisins.
   • Þar sem gildi fylgnistuðuls er jákvætt er jákvæð fylgni milli breytanna „x“ og „y“. Það er, þegar verðmæti „x“ eykst, eykst einnig gildið „y“.
   • Þar sem gildi fylgnistuðilsins er mjög nálægt +1, eru gildi breytanna „x“ og „y“ mjög í samræmi. Ef þú setur punkta á hnitaplanið verða þeir staðsettir nálægt einhverri beinni línu.

Aðferð 2 af 4: Notkun reiknivéla á netinu til að reikna fylgnistuðulinn

1. 1 Finndu reiknivél á netinu til að reikna fylgnistuðulinn. Þessi stuðull er oft reiknaður út í tölfræði. Ef það eru mörg tölupör er nánast ómögulegt að reikna fylgnistuðulinn handvirkt. Þess vegna eru til reiknivélar á netinu til að reikna fylgnistuðulinn. Sláðu inn "fylgnistuðul reiknivél" í leitarvél (án gæsalappa).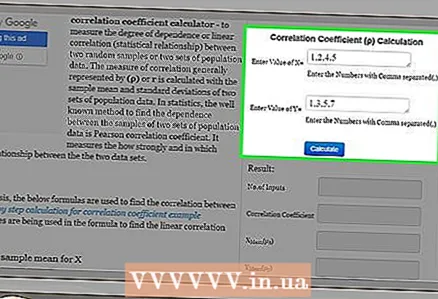
2. 2 Sláðu inn gögn. Athugaðu leiðbeiningarnar á vefsíðunni til að slá inn rétt gögn (tölustafir). Nauðsynlegt er að slá inn viðeigandi tölupör; annars færðu ranga niðurstöðu. Mundu að mismunandi vefsíður hafa mismunandi inntakssnið.
   • Til dæmis, á http://ncalculators.com/statistics/correlation-coefficient-calculator.htm, eru gildi breytanna x og y færð inn í tvær láréttar línur. Gildin eru aðgreind með kommum. Það er, í dæminu okkar, eru gildin „x“ slegin inn þannig: 1,2,4,5 og gildin „y“ svona: 1,3,5,7.
   • Á annarri síðu, http://www.alcula.com/calculators/statistics/correlation-coefficient/, eru gögn færð lóðrétt; í þessu tilfelli, ekki rugla saman samsvarandi tölupörum.
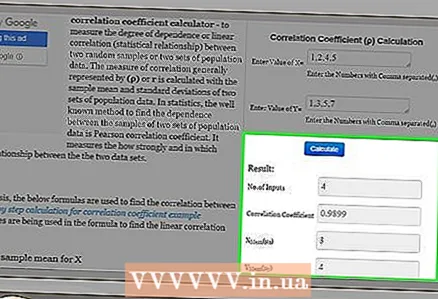3. 3 Reiknaðu fylgnistuðulinn. Eftir að þú hefur slegið inn gögnin, smelltu einfaldlega á „Reikna“, „Reikna“ eða svipaðan hnapp til að fá niðurstöðuna.

Aðferð 3 af 4: Notkun grafreiknivél

1. 1 Sláðu inn gögn. Taktu grafreiknivél, farðu í tölfræðilega útreikningsstillingu og veldu stjórnina „Breyta“.
   • Mismunandi reiknivélar krefjast þess að ýta á mismunandi takka. Þessi grein fjallar um Texas Instruments TI-86 reiknivélina.
   • Ýttu á [2nd] - Stat (fyrir ofan + takkann) til að fara í tölfræðilega útreikningsstillinguna. Ýttu síðan á F2 - Breyta.
2. 2 Eyða fyrri vistuðu gögnum. Flestir reiknivélar geyma tölfræðina sem þú slærð inn þar til þú eyðir þeim. Til að forðast að rugla saman gömlum gögnum og nýjum skaltu fyrst eyða öllum geymdum upplýsingum.
   • Notaðu örvatakkana til að færa bendilinn og auðkenna fyrirsögnina 'xStat'. Ýttu síðan á Hreinsa og Sláðu inn til að hreinsa öll gildi sem eru færð í xStat dálkinn.
   • Notaðu örvatakkana til að auðkenna fyrirsögnina 'yStat'. Ýttu síðan á Hreinsa og Sláðu inn til að hreinsa öll gildi sem eru færð í yStat dálkinn.
3. 3 Sláðu inn upphafleg gögn. Notaðu örvatakkana til að færa bendilinn í fyrsta reitinn undir fyrirsögninni "xStat". Sláðu inn fyrsta gildið og ýttu á Enter. Neðst á skjánum birtist „xStat (1) = __“ þar sem inngefið gildi kemur í stað bils. Eftir að þú ýtir á Enter birtist gildið í töflunni og bendillinn fer í næstu línu; þetta mun sýna "xStat (2) = __" neðst á skjánum.
   • Sláðu inn öll gildi fyrir breytuna "x".
   • Þegar þú hefur slegið inn öll gildi fyrir x skaltu nota örvatakkana til að fara í yStat dálkinn og slá inn gildin fyrir y.
   • Þegar þú hefur slegið inn öll númerapör ýtirðu á Hætta til að hreinsa skjáinn og hætta við samanlögunarham.
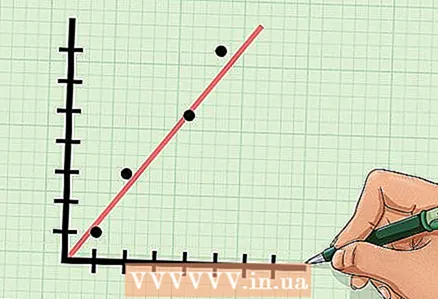
4. 4 Reiknaðu fylgnistuðulinn. Það einkennir hve gögnin eru nálægt ákveðinni beinni línu. Reiknivélin getur fljótt ákvarðað viðeigandi beina línu og reiknað út fylgnistuðulinn.
   • Smelltu á Stat - Calc. Ýttu á [2nd] - [Stat] - [F1] á TI -86.
   • Veldu línulega aðhvarfsaðgerð. Ýtið á [F3] á TI-86 sem er merkt „LinR“. Á skjánum birtist línan „LinR _“ með blikkandi bendli.
   • Sláðu nú inn nöfn tveggja breytna: xStat og yStat.
     • Opnaðu lista yfir nöfn á TI-86; til að gera þetta, ýttu á [2nd] - [List] - [F3].
     • Fyrirliggjandi breytur birtast á botnlínu skjásins. Veldu [xStat] (þú þarft líklega að ýta á F1 eða F2 til að gera þetta), sláðu inn kommu og veldu síðan [yStat].
     • Ýttu á Enter til að vinna úr innsláttargögnum.
5. 5 Greindu niðurstöður þínar. Með því að ýta á Enter birtir skjárinn eftirfarandi upplýsingar:
   • ${ displaystyle y = a + bx}$: þetta er fallið sem lýsir línunni. Vinsamlegast athugaðu að aðgerðin er ekki skrifuð á stöðluðu formi (y = kx + b).
   • ${ displaystyle a =}$... Þetta er y-hnit gatnamóta beinnar línu við y-ásinn.
   • ${ displaystyle b =}$... Þetta er halli línunnar.
   • ${ displaystyle { text {corr}} =}$... Þetta er fylgnistuðullinn.
   • ${ displaystyle n =}$... Þetta er fjöldi tölustafanna sem notuð voru við útreikningana.

Aðferð 4 af 4: Að útskýra grunnhugtök

1. 1 Skilja hugtakið fylgni. Fylgni er tölfræðilegt samband milli tveggja stærða. Fylgnisstuðullinn er tölulegt gildi sem hægt er að reikna út fyrir öll tvö gagnasöfn. Gildi fylgistuðilsins er alltaf á bilinu -1 til +1 og einkennir hve mikið samband er á milli tveggja breytna.
   • Til dæmis miðað við hæð og aldur barna (um 12 ára). Líklegast verður sterk jákvæð fylgni því börn verða hærri með aldrinum.
   • Dæmi um neikvæða fylgni: refsisekúndur og tími sem fer í skíðaskotþjálfun, það er að því meira sem íþróttamaður æfir, því færri vítasekúndur verða gefnar.
   • Að lokum er stundum mjög lítil fylgni (jákvæð eða neikvæð), svo sem á milli skóstærð og stærðfræðitölur.
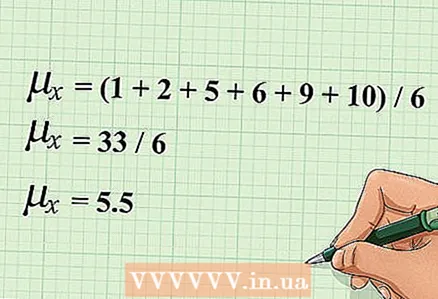2. 2 Mundu hvernig á að reikna reiknimeðal. Til að reikna reikningsmeðaltalið (eða meðaltalið) þarftu að finna summu allra þessara gilda og deila því síðan með fjölda gilda. Mundu að reikningsmeðaltalið er nauðsynlegt til að reikna fylgnistuðulinn.
   • Meðalgildi breytu er gefið til kynna með bókstaf með láréttri stiku fyrir ofan hana. Til dæmis, þegar um breyturnar „x“ og „y“ er að ræða, eru meðalgildi þeirra táknuð sem hér segir: x̅ og y̅. Meðaltalið er stundum táknað með gríska bókstafnum „μ“ (mu). Til að skrifa reikningsmeðaltal gilda breytunnar „x“, notaðu merkið μ_x eða μ (x).
   • Til dæmis, gefið eftirfarandi gildi fyrir breytuna "x": 1,2,5,6,9,10. Reikningsmeðaltal þessara gilda er reiknað út á eftirfarandi hátt:
     • ${ displaystyle mu _ {x} = (1 + 2 + 5 + 6 + 9 + 10) / 6}$
     • ${ displaystyle mu _ {x} = 33/6}$
     • ${ displaystyle mu _ {x} = 5.5}$
3. 3 Takið eftir mikilvægi staðalfráviksins. Í tölfræði einkennir staðalfrávikið að hve miklu leyti tölurnar dreifast miðað við meðaltal þeirra. Ef staðalfrávikið er lítið eru tölurnar nálægt meðaltalinu; ef staðalfrávikið er stórt eru tölurnar langt frá meðaltalinu.
   • Staðalfrávik er gefið til kynna með bókstafnum "s" eða gríska bókstafnum "σ" (sigma). Þannig er staðalfrávik gilda breytunnar „x“ táknað sem hér segir: s_x eða σ_x.
4. 4 Mundu eftir tákninu fyrir samantektaraðgerðina. Samantektartáknið er eitt algengasta táknið í stærðfræði og gefur til kynna summa gilda. Þetta tákn er gríski bókstafurinn „Σ“ (hástafur sigma).
   • Til dæmis, ef gefin eru eftirfarandi gildi breytunnar „x“: 1,2,5,6,9,10, þá þýðir Σx:
     • 1 + 2 + 5 + 6 + 9 + 10 = 33.

Ábendingar

• Fylgnisstuðullinn er stundum kallaður „Pearson fylgistuðull“ eftir þróunaraðila sínum Carl Pearson.
• Í flestum tilfellum, þegar fylgnistuðullinn er meiri en 0,8 (jákvæður eða neikvæður), er sterk fylgni; ef fylgnistuðullinn er minni en 0,5 (jákvæður eða neikvæður) sést veik fylgni.

Viðvaranir

• Fylgni einkennir sambandið milli gilda tveggja breytna. En mundu að fylgni hefur ekkert að gera með orsakasamhengi. Til dæmis, ef þú berð saman hæð og skóstærð fólks, þá er líklegt að þú finnir sterka jákvæða fylgni. Almennt, því hærri sem manneskjan er, því stærri er skóstærðin. En þetta þýðir ekki að hækkun á hæð leiði til sjálfvirkrar skóstærðar eða að stærri fætur leiði til hraðari vaxtar. Þetta magn er einfaldlega innbyrðis tengt.