Efni.

• Að stíga
• Aðferð 1 af 3: Nota radíusformúlur
• Aðferð 2 af 3: Skilgreindu lykilhugtök
• Aðferð 3 af 3: Finndu radíusinn sem fjarlægðina milli tveggja punkta
• Ábendingar

Radíus kúlu (skammstafað sem breytan r eða R.) er fjarlægðin frá nákvæmri miðju kúlunnar að punkti á yfirborði þess kúlu. Eins og með hringi er radíus kúlunnar oft nauðsynleg mælikvarði til að reikna út þvermál, ummál, flatarmál og rúmmál kúlunnar. Hins vegar er einnig hægt að vinna afturábak frá þvermáli, ummáli osfrv til að finna radíus kúlunnar. Notaðu formúluna sem er viðeigandi fyrir þau gögn sem þú hefur.

Að stíga

Aðferð 1 af 3: Nota radíusformúlur

1. Finndu radíusinn ef þú veist þvermálið. Radíusinn er hálfur í þvermál, svo þú notar formúluna r = D / 2. Þetta er eins og aðferðin við útreikning á radíus hrings þar sem þvermálið er gefið upp.
   • Ef þú ert með kúlu með 16 cm þvermál reiknarðu út radíusinn með 16/2 = 8 cm. Ef þvermálið er 42, þá er radíusinn 21.
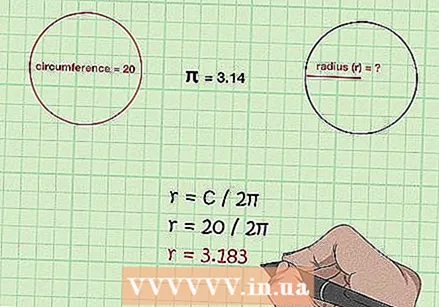2. Finndu radíusinn ef þú veist ummálið. Notaðu formúluna C / 2π. Þar sem ummálið er jafnt og πD, sem aftur er jafnt og 2πr, reiknið radíusinn með því að deila ummálinu með 2π.
   • Ef þú ert með kúlu með 20 m ummál, finnur þú radíusinn með 20 / 2π = 3,183 m.
   • Þú getur notað sömu formúlu til að umbreyta á milli radíus og ummáls hrings.
3. Reiknaðu radíusinn ef þú veist um rúmmál kúlunnar. Notaðu formúluna ((V / π) (3/4)). Rúmmál kúlu er dregið af jöfnunni V = (4/3) πr. Með því að leysa jöfnuna fyrir r færðu ((V / π) (3/4)) = r, svo það verður ljóst að radíus a eða kúlu er jafn rúmmálinu deilt með π, sinnum 3/4, til 1/3 máttur (eða teningarót).
   • Ef þú ert með kúlu með 100 cm rúmmál færðu radíusinn sem hér segir:
     • ((V / π) (3/4)) = r
     • ((100 / π) (3/4)) = r
     • ((31.83) (3/4)) = r
     • (23,87) = r
     • 2,88 = r
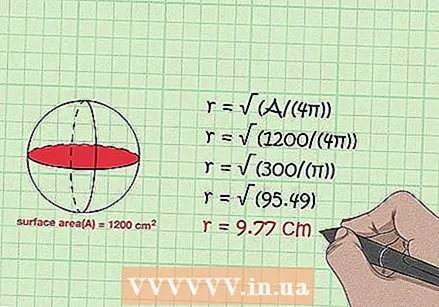4. Finndu radíus yfirborðsins. Notaðu formúluna r = √ (A / (4π)). Þú reiknar flatarmál kúlu með jöfnu A = 4πr. Að leysa jöfnuna fyrir r gefur √ (A / (4π)) = r, sem þýðir að radíus kúlunnar er jafnt ferningsrót flatarmálsins deilt með 4π. Þú getur einnig knúið (A / (4π)) í 1/2 fyrir sömu niðurstöðu.
   • Ef þú ert með kúlu með flatarmálið 1200 cm reiknarðu radíusinn á eftirfarandi hátt:
     • √ (A / (4π)) = r
     • √ (1200 / (4π)) = r
     • √ (300 / (π)) = r
     • √ (95,49) = r
     • 9,77 sm = r

Aðferð 2 af 3: Skilgreindu lykilhugtök

1. Þekktu grunnvíddir kúlu. Radíusinn (r) er fjarlægðin frá nákvæmri miðju kúlunnar að hvaða punkti sem er á yfirborði kúlunnar. Almennt er hægt að finna geisla kúlu ef þú veist um þvermál, ummál, rúmmál eða svæði.
   • Þvermál (D): lengd línunnar í gegnum miðju kúlu & ndash; tvöfalda radíusinn. Þvermálið er lengd línu í gegnum miðju kúlunnar, frá einum punkti utan á kúlunni að samsvarandi punkti beint á móti henni. Með öðrum orðum, mesta mögulega fjarlægðin milli tveggja punkta á kúlunni.
   • Ummál (C): einvíddar fjarlægðin umhverfis kúluna á breiðasta punkti hennar. Með öðrum orðum, ummál hringlaga þversniðs kúlu, en plan hennar liggur í gegnum miðju kúlunnar.
   • Magn (V): þrívíða rýmið innan kúlunnar. Það er „rýmið sem kúlan tekur“.
   • Yfirborð (A): tvívíða rýmið á ytra yfirborði kúlunnar. Magnið á flatu rými sem hylur utan á kúluna.
   • Pi (π): stöðugt sem lýsir hlutfalli ummáls hringsins og þvermáls hringsins. Fyrstu 10 tölustafir Pi eru alltaf 3,141592653, þó að þetta sé venjulega ávalið að 3,14.
2. Notaðu mismunandi mælingar til að ákvarða radíus. Þú getur notað þvermál, ummál, rúmmál og svæði til að reikna út radíus kúlu. Ef þú veist lengd geislans geturðu reiknað hvaða af þessum tölum sem er. Svo til að finna radíusinn geturðu snúið formúlunum við útreikning á þessum hlutum. Lærðu radíusformúlurnar til að reikna þvermál, ummál, flatarmál og rúmmál.
   • D = 2r. Eins og með hringi er þvermál kúlu tvöfaldur radíus.
   • C = πD eða 2πr. Eins og með hringi er ummál kúlu jafnt π sinnum þvermál þess. Þar sem þvermálið er tvöfalt radíus getum við líka sagt að ummálið sé tvöfalt radíus sinnum π.
   • V = (4/3) πr. Rúmmál kúlu er radíus að rúmmetri (r x r x r), sinnum π, sinnum 4/3.
   • A = 4πr. Flatarmál kúlunnar er radíus í krafti tveggja (rxr) sinnum π, sinnum 4. Þar sem ummál hrings er πr, má einnig segja að flatarmál kúlunnar sé jafnt fjórum sinnum svæði hringsins, eins og það myndast af ummáli þess.

Aðferð 3 af 3: Finndu radíusinn sem fjarlægðina milli tveggja punkta

1. Finndu hnitin (x, y, z) miðju kúlunnar. Ein leið til að hugsa um radíus kúlunnar er eins og fjarlægðin milli miðju kúlunnar og hvaða punkt sem er á yfirborði hennar. Vegna þess að þetta er satt er hægt að nota hnit miðju og punkt á yfirborði kúlunnar til að ákvarða radíus kúlunnar með því að reikna fjarlægðina milli tveggja punkta með því að nota tilbrigði við venjulegu fjarlægðarformúluna. Til að byrja skaltu finna hnit miðju kúlunnar. Athugaðu að kúla er þrívídd, hún verður punktur (x, y, z) í stað punktar (x, y).
   • Þetta er auðveldara að skilja með dæmi. Segjum sem svo að kúla sé gefin með sem miðju (-1, 4, 12). Í næstu skrefum ætlum við að nota þennan punkt við að ákvarða radíus.
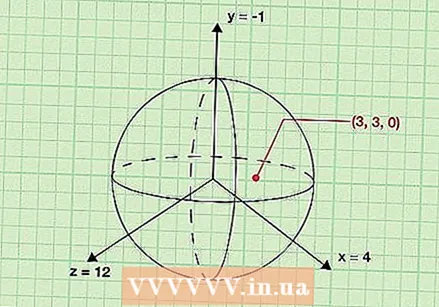2. Finndu hnit punktar á yfirborði kúlunnar. Þá þarftu að ákvarða (x, y, z) hnit punktar á yfirborði kúlunnar. Þetta er mögulegt hver benda á yfirborð kúlunnar. Vegna þess að samkvæmt skilgreiningu eru allir punktar á yfirborði kúlu jafnt frá miðju, getur þú notað hvaða punkt sem er til að ákvarða radíus.
   • Í samhengi við dæmið okkar, gerum við það að aðalatriðinu (3, 3, 0) á yfirborði kúlunnar. Með því að reikna fjarlægðina milli þessa punkta og miðju getum við fundið radíusinn.
3. Finndu radíusinn með formúlunni d = √ ((x₂ - x₁) + (y₂ - y₁) + (z₂ - z₁)). Nú þegar þú þekkir miðju kúlunnar og punkt á yfirborði kúlunnar geturðu fundið út radíusinn með því að reikna fjarlægðina á milli þeirra. Notaðu þrívíðu fjarlægðarformúluna d = √ ((x₂ - x₁) + (y₂ - y₁) + (z₂ - z₁)), þar sem d er fjarlægðin, (x₁, y₁, z₁) táknar hnit miðjunnar og (x₂, y₂, z₂) táknar hnit punktsins á yfirborðinu til að ákvarða fjarlægðina milli tveggja punkta.
   • Í dæminu okkar skiptum við (4, -1, 12) fyrir (x₁, y₁, z₁) og (3, 3, 0) fyrir (x₂, y₂, z₂) og leysa þetta á eftirfarandi hátt:
     • d = √ ((x₂ - x₁) + (y₂ - y₁) + (z₂ - z₁))
     • d = √ ((3 - 4) + (3 - -1) + (0 - 12))
     • d = √ ((- 1) + (4) + (-12))
     • d = √ (1 + 16 + 144)
     • d = √ (161)
     • d = 12,69. Þetta er geisli kúlunnar okkar.
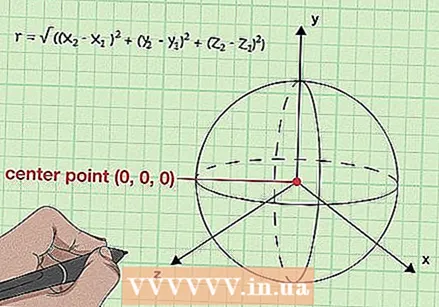4. Almennt, veistu að r = √ ((x₂ - x₁) + (y₂ - y₁) + (z₂ - z₁)). Í kúlu hefur hver punktur á yfirborðinu sömu fjarlægð frá miðju kúlunnar. Með því að taka ofangreinda þrívíddarfjarlægðarformúlu og skipta um breytuna „d“ fyrir breytuna „r“ geislans fáum við jöfnu sem gerir okkur kleift að finna radíusinn við hvaða miðpunkt sem er (x₁, y₁, z₁) og hvaða samsvarandi punkt á yfirborðinu (x₂, y₂, z₂).
   • Með því að ferma báðar hliðar þessarar jöfnu fáum við: r = (x₂ - x₁) + (y₂ - y₁) + (z₂ - z₁). Athugið: Þetta er í meginatriðum það sama og staðalljöfnun kúlu (r = x + y + z), miðað við að miðjan sé jöfn (0,0,0).

Ábendingar

• Röð aðgerða er mikilvæg. Ef þú ert ekki viss um hvernig reiknireglurnar virka og reiknivélin þín styður sviga, vertu viss um að nota þau.
• Þessi grein var búin til vegna þess að þetta efni var mjög eftirsótt. Hins vegar, ef þú ert að reyna að skilja landfræðilega rúmfræði í fyrsta skipti, er líklega betra að byrja á hinni hliðinni: að reikna út eiginleika kúlu þegar radíus er gefinn.
• Pi eða π er grískur stafur sem gefur til kynna hlutfall þvermáls hrings og ummáls. Það er óskynsamleg tala og er ekki hægt að skrifa sem hlutfall rauntala. Það eru margar áætlanir og 333/106 skilar pi fjórum aukastöfum. Í dag muna flestir eftir nálgun 3.14 sem venjulega er nógu nákvæm í hversdagslegum tilgangi.