Höfundur:
Judy Howell
Sköpunardag:
2 Júlí 2021
Uppfærsludagsetning:
1 Júlí 2024
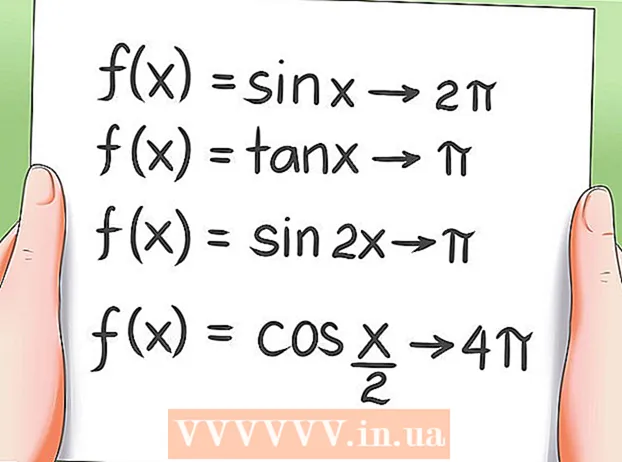
Efni.
Þríhyrnds jöfna er jöfnu með einni eða fleiri þríhyrndaraðgerðum breytu þríhyrningsferilsins x. Að leysa fyrir x þýðir að finna gildi þríhyrningsferla þar sem þríhyrningsfræðilegar aðgerðir valda því að þríhyrningsjöfnu er sönn.
- Svör eða gildi lausnarferlanna eru gefin upp í gráðum eða radíönum. Dæmi:
x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 gráður; x = 37,12 gráður; x = 178,37 stig
- Athugasemd: Í einingarhringnum eru þrístigsaðgerðir hverrar ferils jafnar og þríhyrningsaðgerðir samsvarandi horns. Einingarhringurinn skilgreinir allar þríhyrningarfræðilegar aðgerðir breytuferilsins x. Það er einnig notað sem sönnun við að leysa grunn jöfnur og ójöfnur.
- Dæmi um þríhyrningajöfnur:
- sin x + sin 2x = 1/2; tan x + vöggu x = 1.732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.
- Einingarhringurinn.
- Þetta er hringur með Radius = 1, þar sem O er upphafið. Einingarhringurinn skilgreinir 4 megin þrígreindaraðgerðir breytu ferilsins x sem hringir hann rangsælis.
- Þegar ferillinn með gildi x er breytilegur á einingahringnum, þá heldur hann:
- Lárétti ásinn OAx skilgreinir þríhyrningsaðgerðina f (x) = cos x.
- Lóðrétti ásinn OBy skilgreinir þríhyrningsaðgerðina f (x) = sin x.
- Lóðrétti ásinn AT skilgreinir þríhyrningsaðgerðina f (x) = tan x.
- Lárétti ásinn BU skilgreinir þríhyrningsaðgerðina f (x) = vöggu x.
- Einingahringurinn er einnig notaður til að leysa grundvallar þríhyrndar jöfnur og staðlaða þríhyrninga ójöfnuð með því að taka tillit til hinna ýmsu staða ferilsins x á hringnum.
Að stíga
 Skilja lausnaraðferðina.
Skilja lausnaraðferðina.- Til að leysa þríhyrningsjöfnu breytir þú henni í eina eða fleiri grunnjöfnur. Að leysa þríhyrningsjöfnur leiðir að lokum til þess að leysa 4 grundvallar jöfnur.
 Vita hvernig á að leysa grundvallar þríhyrningajöfnur.
Vita hvernig á að leysa grundvallar þríhyrningajöfnur.- Það eru 4 grundvallar þríhyrndar jöfnur:
- sin x = a; cos x = a
- tan x = a; vöggu x = a
- Þú getur leyst grundvallar jöfnur með þrístæðu mælikvarða með því að rannsaka ýmsar stöður ferilsins x á þríhyrningahringnum og með því að nota þríhyrningsbreytitöflu (eða reiknivél). Til að skilja að fullu hvernig hægt er að leysa þessar og svipaðar grunnstigstærðarjöfnur, lestu eftirfarandi bók: „Þrístigsfræði: Lausn þrístigsstigsjöfna og ójöfnur“ (Amazon E-bók 2010).
- Dæmi 1. Leysa fyrir sin x = 0,866. Viðskiptataflan (eða reiknivélin) gefur svarið: x = Pi / 3. Þríhyrningahringurinn gefur aðra feril (2Pi / 3) með sama gildi fyrir sinusinn (0,866). Þríhyrningahringurinn býður einnig upp á óendanleg svör sem kallast aukin svör.
- x1 = Pi / 3 + 2k.Pi, og x2 = 2Pi / 3. (Svar innan tímabils (0, 2Pi))
- x1 = Pi / 3 + 2k Pi, og x2 = 2Pi / 3 + 2k Pi. (Ítarleg svör).
- Dæmi 2. Leysið: cos x = -1/2. Reiknivélar gefa x = 2 Pi / 3. Þríhyrndur hringur gefur einnig x = -2Pi / 3.
- x1 = 2Pi / 3 + 2k.Pi, og x2 = - 2Pi / 3. (Svör fyrir tímabil (0, 2Pi))
- x1 = 2Pi / 3 + 2k Pi, og x2 = -2Pi / 3 + 2k.Pi. (Útbreidd svör)
- Dæmi 3. Laus: tan (x - Pi / 4) = 0.
- x = Pi / 4; (Svar)
- x = Pi / 4 + k Pi; (Útvíkkað svar)
- Dæmi 4. Leysa: Cot 2x = 1.732. Reiknivélar og þríhyrndur hringur gefa:
- x = Pi / 12; (Svar)
- x = Pi / 12 + k Pi; (Útbreidd svör)
 Lærðu umbreytingarnar sem notaðar eru við að leysa þríhyrningsjöfnur.
Lærðu umbreytingarnar sem notaðar eru við að leysa þríhyrningsjöfnur.- Til að umbreyta tiltekinni þríhyrningsjöfnu í venjulegar þríhyrningajöfnur, notaðu staðlaðar algebru ummyndanir (þáttunarstig, sameiginlegur þáttur, margliður ...), skilgreiningar og eiginleikar þríhyrningsaðgerða og þríhyrningseiningar. Það eru um það bil 31, 14 sem eru þríhyrndar sjálfsmyndir, frá 19 til 31, einnig kallaðar umbreytingarauðkenningar, vegna þess að þær eru notaðar við umbreytingu þríhyrnings jöfna. Sjá ofangreinda bók.
- Dæmi 5: Hægt er að breyta þríhyrnds jöfnu: sin x + sin 2x + sin 3x = 0 í afurð úr jöfnum þríhyrningajöfnum með því að nota þríhyrningseiningar: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Grundvallar þríhyrndar jöfnur til að leysa eru: cos x = 0; sin (3x / 2) = 0; og cos (x / 2) = 0.
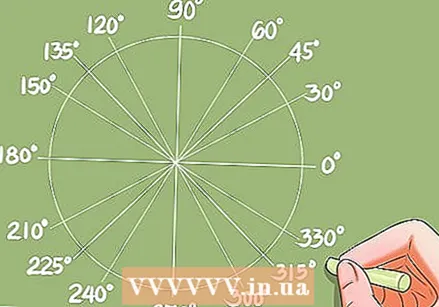 Finndu línurnar sem þríhyrndar aðgerðir eru þekktar fyrir.
Finndu línurnar sem þríhyrndar aðgerðir eru þekktar fyrir.- Áður en þú getur lært hvernig á að leysa þríhyrningsjöfnur þarftu að vita hvernig á fljótt að finna þær sveigjur sem þríhyrndar aðgerðir eru þekktar fyrir. Viðskiptagildi ferla (eða horn) er hægt að ákvarða með þríhyrningstöflu eða reiknivél.
- Dæmi: Leysa fyrir cos x = 0,732. Reiknivélin gefur lausnina x = 42,95 gráður. Einingarhringurinn gefur aðrar sveigjur með sama gildi fyrir kósínusinn.
 Teiknið bogann af svarinu á einingahringinn.
Teiknið bogann af svarinu á einingahringinn.- Þú getur búið til línurit til að skýra lausnina á einingahringnum. Lokapunktar þessara sveigja eru reglulegar marghyrningar á þríhyrningahringnum. Nokkur dæmi:
- Endapunktar ferilsins x = Pi / 3 + k. Pi / 2 er ferningur á einingahringnum.
- Ferlar x = Pi / 4 + k.Pi / 3 eru táknaðir með hnit sexhyrnings á einingarhringnum.
 Lærðu hvernig á að leysa þríhyrningajöfnur.
Lærðu hvernig á að leysa þríhyrningajöfnur.- Ef tilgreind þríhyrningsjöfna inniheldur aðeins eina þríhyrningsaðgerð skaltu leysa hana sem hefðbundna þríhyrningsjöfnu. Ef tilgreind jöfnu inniheldur tvö eða fleiri þríhyrningsfræðilegar aðgerðir, eru til tvær lausnaraðferðir, allt eftir möguleikum til að umbreyta jöfnu.
- A. Aðferð 1.
- Breyttu þríhyrningsjöfnunni í framleiðslu á forminu: f (x) .g (x) = 0 eða f (x) .g (x) .h (x) = 0, þar sem f (x), g (x) og h (x) eru þríhyrndar jöfnur.
- Dæmi 6. Leysið: 2cos x + sin 2x = 0. (0 x 2Pi)
- Lausn. Skiptu um sin 2x í jöfnunni með því að nota sjálfsmyndina: sin 2x = 2 * sin x * cos x.
- cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Leystu síðan 2 staðlaðar þríhyrningsaðgerðir: cos x = 0, og (sin x + 1) = 0.
- Dæmi 7. Leysa: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
- Lausn: Breyttu þessu í vöru með því að nota þríhyrningseiningarnar: cos 2x (2cos x + 1) = 0. Leystu nú 2 grunnstigstigjafna: cos 2x = 0 og (2cos x + 1) = 0.
- Dæmi 8. Leysa: sin x - sin 3x = cos 2x. (0 x 2Pi)
- Lausn: Breyttu þessu í vöru með því að nota þríhyrningsfræðilegar auðkenni: -cos 2x * (2sin x + 1) = 0. Leystu nú 2 grunnstigstigjafna: cos 2x = 0, og (2sin x + 1) = 0.
- B. Aðferð 2.
- Breytir trig jöfnu í trig jöfnu þar sem aðeins ein einstök trig virka sem breytu. Það eru nokkur ráð um hvernig á að velja viðeigandi breytu. Algengar breytur eru: sin x = t; cos x = t; cos 2x = t, tan x = t og tan (x / 2) = t.
- Dæmi 9. Leysa: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
- Lausn. Í jöfnunni, skipta um (cos ^ 2x) fyrir (1 - sin ^ 2x) og einfalda jöfnuna:
- 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Notaðu nú sin x = t. Jafnan verður: 5t ^ 2 - 4t - 9 = 0. Þetta er veldisjafna með 2 rætur: t1 = -1 og t2 = 9/5. Við getum hafnað seinni t2, vegna þess að> 1. Leysum núna fyrir: t = sin = -1 -> x = 3Pi / 2.
- Dæmi 10. Leysa: tan x + 2 tan ^ 2 x = barnarúm x + 2.
- Lausn. Notaðu tan x = t. Breyttu jöfnunni í jöfnu með t sem breytu: (2t + 1) (t ^ 2 - 1) = 0. Leysið fyrir t úr þessari vöru, leysið síðan stöðluðu þríhyrningsjöfnuna tan x = t fyrir x.
- Ef tilgreind þríhyrningsjöfna inniheldur aðeins eina þríhyrningsaðgerð skaltu leysa hana sem hefðbundna þríhyrningsjöfnu. Ef tilgreind jöfnu inniheldur tvö eða fleiri þríhyrningsfræðilegar aðgerðir, eru til tvær lausnaraðferðir, allt eftir möguleikum til að umbreyta jöfnu.
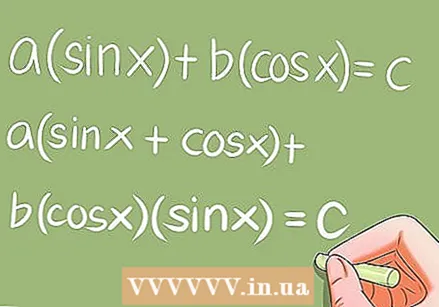 Leysa sérstök þríhyrningsjöfnur.
Leysa sérstök þríhyrningsjöfnur.- Það eru nokkrar sérstakar þríhyrningsjöfnur sem krefjast nokkurra sérstakra umbreytinga. Dæmi:
- a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
- a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
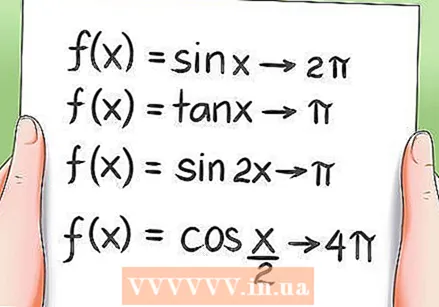 Lærðu reglubundna eiginleika þrígreindra aðgerða.
Lærðu reglubundna eiginleika þrígreindra aðgerða.- Allar þríhyrningsaðgerðir eru reglubundnar, sem þýðir að þær fara aftur í sama gildi eftir snúning yfir tímabil. Dæmi:
- Fallið f (x) = sin x hefur 2Pi sem punkt.
- Fallið f (x) = tan x hefur Pi sem tímabil.
- Fallið f (x) = sin 2x hefur Pi sem tímabil.
- Fallið f (x) = cos (x / 2) hefur 4Pi sem tímabil.
- Ef tímabilið er tilgreint í æfingunum / prófinu, þá þarftu bara að finna kúrfuna (r) x innan þessa tímabils.
- ATH: Að leysa þríhyrningsjöfnur er erfiður og leiðir oft til villna og mistaka. Þess vegna ætti að kanna svör vandlega. Eftir lausn er hægt að athuga svörin með því að nota reiknivél fyrir beina framsetningu þríhyrndar jöfnu R (x) = 0. Svarin (sem ferningsrót) eru gefin með aukastöfum. Sem dæmi hefur Pi gildi 3,14
- Allar þríhyrningsaðgerðir eru reglubundnar, sem þýðir að þær fara aftur í sama gildi eftir snúning yfir tímabil. Dæmi: