Efni.

• Skref
• Hluti 1 af 3: Einfaldleikapróf
• 2. hluti af 3: Hvernig einfaldleikapróf virka
• Hluti 3 af 3: Notkun kínversku leifasetningarinnar
• Ábendingar
• Hvað vantar þig

Aðaltölur eru tölur sem eru aðeins deilanlegar sjálfum sér og með 1. Allar aðrar tölur eru kallaðar samsettar tölur. Það eru margar leiðir til að ákvarða hvort tala sé frumtala og þær hafa allar sína kosti og galla. Annars vegar eru sumar aðferðirnar mjög nákvæmar, en þær eru frekar flóknar ef þú ert að fást við mikla tölu. Á hinn bóginn eru miklu hraðari leiðir en þær geta leitt til rangra niðurstaðna. Val á viðeigandi aðferð fer eftir því hversu stórar tölur þú ert að vinna með.

Skref

Hluti 1 af 3: Einfaldleikapróf

Athugið: í öllum formúlum n táknar númerið sem á að athuga.

1. 1 Upptalning deiliskipta. Það er nóg að skipta n að öllum frumtölum frá 2 að ávölnu gildinu (${ displaystyle { sqrt {n}}}$).
2. 2 Fermats litla setning. Viðvörun: stundum mun prófið ranglega bera kennsl á samsettar tölur sem frumtölur, jafnvel fyrir öll gildi a.
   • Við skulum velja heiltölu aþannig að 2 ≤ a ≤ n - 1.
   • Ef a (mod n) = a (mod n) þá er talan líklega frumtala. Ef jafnrétti er ekki fullnægt er talan n samsett.
   • Athugaðu gefið jafnrétti fyrir mörg gildi aað auka líkurnar á því að fjöldinn sem er prófaður sé örugglega frábær.
3. 3 Miller-Rabin próf. Viðvörun: stundum, þó sjaldan, fyrir mörg gildi a, mun prófið ranglega bera kennsl á samsettar tölur sem frumtölur.
   • Finndu magn s og d þannig að ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Veldu heiltölu a á bilinu 2 ≤ a ≤ n - 1.
   • Ef a = +1 (mod n) eða -1 (mod n), þá er n líklega frumtali. Farðu í niðurstöðuna í þessu tilfelli. Ef jafnréttið heldur ekki, farðu í næsta skref.
   • Kvaðra svarið þitt (${ displaystyle a ^ {2d}}$). Ef þú færð -1 (mod n), þá er n líklega frumtala. Farðu í niðurstöðuna í þessu tilfelli. Ef jafnrétti bregst skaltu endurtaka (${ displaystyle a ^ {4d}}$ og svo framvegis) þar til ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • Ef í einhverju skrefi eftir að setja aðra tölu en ${ displaystyle pm 1}$ (mod n), þú hefur +1 (mod n), þannig að n er samsett tala. Ef ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), þá er n ekki frumtali.
   • Niðurstaða prófunar: ef n standist prófið skaltu endurtaka það fyrir önnur gildi aað auka sjálfstraustið.

2. hluti af 3: Hvernig einfaldleikapróf virka

1. 1 Upptalning deiliskipta. Samkvæmt skilgreiningu, fjöldinn n er einfalt aðeins ef það er ekki deilanlegt með 2 og öðrum heiltölum nema 1 og sjálfu sér. Ofangreind formúla gerir þér kleift að fjarlægja óþarfa skref og spara tíma: til dæmis, eftir að hafa athugað hvort tala er deilanleg með 3, þarf ekki að athuga hvort hún sé deilanleg með 9.
   • Gólf (x) falla x að næstu heiltölu minni en eða jöfn x.
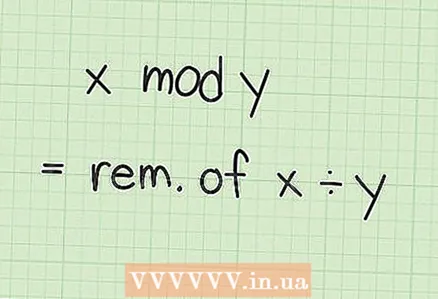2. 2 Lærðu um mátreikninga. Aðgerðin "x mod y" (mod er skammstöfun á latneska orðinu "modulo", það er "mát") þýðir "deila x með y og finna afganginn." Með öðrum orðum, í mátareikningi, þegar komið er að ákveðnu gildi, sem kallað er eining, tölurnar „snúast“ í núll aftur. Til dæmis telur klukkan niður með einingu 12: hún sýnir 10, 11 og 12 klukkustundir og snýr síðan aftur í 1.
   • Margir reiknivélar eru með mod -lykil. Lok þessa kafla sýnir þér hvernig á að reikna þessa aðgerð handvirkt fyrir stórar tölur.
3. 3 Lærðu um gildrur Fermats litlu setningarinnar. Allar tölur sem prófskilyrði eru ekki uppfyllt fyrir eru samsett en restin af tölunum er aðeins líklega eru einfaldar. Ef þú vilt forðast rangar niðurstöður skaltu leita n í listanum yfir „Carmichael tölur“ (samsettar tölur sem fullnægja þessu prófi) og „Fermat gervitölutölur“ (þessar tölur uppfylla prófunarskilyrðin aðeins fyrir sum gildi a).
4. 4 Notaðu Miller-Rabin prófið ef hentugt er. Þó að þessi aðferð sé frekar fyrirferðarmikil við handvirka útreikninga, þá er hún oft notuð í tölvuforritum. Það veitir ásættanlegan hraða og færri villur en aðferð Fermat. Samsett tala verður ekki tekin sem frumtala ef útreikningar eru gerðir fyrir fleiri en ¼ gildi a... Ef þú velur af handahófi mismunandi gildi a og fyrir þá alla mun prófið gefa jákvæða niðurstöðu, við getum gert ráð fyrir því með nokkuð miklu trausti að n er frumtala.
5. 5 Notaðu mátareikninga fyrir stóra tölu. Ef þú ert ekki með reiknivél fyrir hendi eða reiknivélin er ekki hönnuð til að takast á við svona stórar tölur skaltu nota aflareiginleika og mátareikninga til að gera útreikningana auðveldari. Hér að neðan er dæmi um ${ displaystyle 3 ^ {50}}$ mod 50:
   • Endurskrifaðu tjáninguna á þægilegra formi: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Handvirkar útreikningar geta þurft frekari einföldun.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Hér tókum við tillit til eiginleika margfeldisaukningar.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Hluti 3 af 3: Notkun kínversku leifasetningarinnar

1. 1 Veldu tvær tölur. Ein af tölunum verður að vera samsett og hin verður að vera nákvæmlega sú sem þú vilt prófa til einföldunar.
   • Númer 1 = 35
   • Númer 2 = 97
2. 2 Veldu tvö gildi sem eru stærri en núll og hver um sig minni en tölurnar Number1 og Number2. Þessi gildi mega ekki vera þau sömu.
   • Gildi1 = 1
   • Gildi2 = 2
3. 3 Reiknaðu MMI (Mathematical Multiplicative Inverse) fyrir Number1 og Number2.
   • Reiknaðu MMI
     • MMI1 = Number2 ^ -1 Mod Number1
     • MMI2 = Number1 ^ -1 Mod Number2
   • Aðeins fyrir frumtölur (þetta mun gefa númer fyrir samsettar tölur, en það mun ekki vera MMI hans):
     • MMI1 = (Number2 ^ (Number1-2))% Number1
     • MMI2 = (Number1 ^ (Number2-2))% Number2
   • Til dæmis:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Búðu til töflu fyrir hvert MMI niður í log2 einingar:
   • Fyrir MMI1
     • F (1) = Fjöldi2% Fjöldi1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Fjöldi1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Fjöldi1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Fjöldi1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Fjöldi1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Fjöldi1 = 1 * 1% 35 = 1
   • Reiknaðu paraðar tölur 1 - 2
     • 35 -2 = 33 (10001) grunnur 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • Fyrir MMI2
     • F (1) = Fjöldi1% Fjöldi2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Fjöldi2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Number2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Number2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Fjöldi2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Fjöldi2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Fjöldi2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Fjöldi2 = 35 * 35 mod 97 = 61
   • Reiknaðu paraða númer 2 - 2
     • 97 - 2 = 95 = (1011111) grunnur 2
     • MMI2 = (((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Reiknaðu (Value1 * Number2 * MMI1 + Value2 * Number1 * MMI2)% (Number1 * Number2)
   • Svar = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Svar = (2619 + 4270)% 3395
   • Svar = 99
6. 6 Athugaðu að númer1 er ekki frumtala
   • Reiknaðu (svar - gildi1)% tala1
   • 99 – 1 % 35 = 28
   • Þar sem 28 er stærra en 0 er 35 ekki frumtala.
7. 7 Gakktu úr skugga um að númer2 sé frumtala.
   • Reiknaðu (svar - gildi2)% tala2
   • 99 – 2 % 97 = 0
   • Þar sem 0 er 0 er 97 líklegast frumtala.
8. 8 Endurtaktu skref 1 til 7 að minnsta kosti tvisvar sinnum í viðbót.
   • Ef þú færð 0 í þrepi 7:
     • Notaðu annað númer1 ef númer1 er ekki frumtala.
     • Notaðu annað númer1 ef númer1 er frumtala. Í þessu tilfelli ættir þú að fá 0 í skrefum 6 og 7.
     • Notaðu mismunandi merkingu1 og merkingu2.
   • Ef þú færð stöðugt 0 í þrepi 7 þá er mjög líklegt að númer 2 sé frumtali.
   • Skref 1 til og með 7 geta leitt til villu ef númer1 er ekki frumtala og númer2 er deilir númer1. Aðferðin sem lýst er virkar í öllum tilfellum þegar báðar tölurnar eru frumtölur.
   • Ástæðan fyrir því að þú þarft að endurtaka skref 1 til og með 7 er vegna þess að í sumum tilfellum, jafnvel þó að númer1 og númer 2 séu ekki frumtölur, þá færðu 0 (fyrir eina eða báðar tölurnar). Þetta gerist sjaldan.Veldu annað númer1 (samsett), og ef númer2 er ekki frumtala, þá mun númer2 ekki vera núll í þrepi 7 (nema þegar talan1 er deilir tölu2 - hér verða frumtalan alltaf jafn núll í þrepi 7).

Ábendingar

• Aðaltölur frá 168 til 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Þrátt fyrir að grimmdarpróf sé leiðinlegt próf þegar unnið er með stórar tölur, þá er það nokkuð skilvirkt fyrir litlar tölur. Jafnvel þegar um er að ræða stórar tölur, byrjaðu á því að prófa litla deiliskipta og farðu síðan yfir í flóknari aðferðir til að athuga einfaldleika talna (ef litlar deilur finnast ekki).

Hvað vantar þig

• Pappír, penni eða tölva