Efni.

• Skref

Veistu ekki hvernig á að vinna með lógaritma? Ekki hafa áhyggjur! Það er ekki svo erfitt. Logaritminn er skilgreindur sem veldisvísir, það er logarithmic equation log_ax = y jafngildir veldisvísu jöfnunni a = x.

Skref

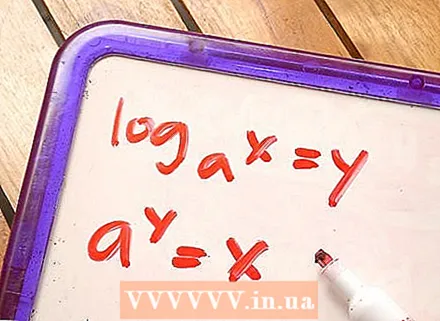1. 1 Mismunur á milli logaritmískrar og veldisvísis jöfnu. Ef jöfnan inniheldur lógaritm þá er hún kölluð lógaritmísk jöfnu (til dæmis log_ax = y). Logaritminn er táknaður með log. Ef jöfnu inniheldur gráðu og vísir hennar er breytu, þá er það kallað veldisstuðul jafna.
   • Logaritmísk jöfnu: log_ax = y
   • Vísitölujöfnur: a = x
2. 2 Hugtakafræði. Í logaritmaskránni₂8 = 3 tala 2 er grunnur logaritmsins, tala 8 er rök logaritmsins, tala 3 er gildi logaritmsins.
3. 3 Mismunur á aukastaf og náttúrulegum lógaritmum.
   • Desimal lógaritmar eru lógaritmar með grunn 10 (t.d. log₁₀x). Logaritminn, skrifaður sem log x eða lg x, er aukastaf lógaritminn.
   • Náttúrulegir logaritmar eru lógaritmar með grunn "e" (til dæmis log_ex). „E“ er stærðfræðilegur fasti (tala Eulers) sem er jöfn mörkunum (1 + 1 / n) þar sem n hefur tilhneigingu til óendanleika. „E“ er um það bil 2,72. Logaritminn, skrifaður sem ln x, er hinn náttúrulegi logaritmi.
   • Aðrir lógaritmar... Grunn 2 lógaritmar eru kallaðir tvöfaldir (til dæmis log₂x). Grunn 16 lógaritmar eru kallaðir hexadecimal (til dæmis log₁₆x eða log_{# 0f}x). Grunn 64 lógaritmar eru svo flóknir að þeir lúta aðlögunarfræðilegri geometrískri nákvæmni (ACG).
4. 4 Eiginleikar lógaritma. Eiginleikar lógaritma eru notaðir til að leysa lógaritmíska og veldisbundna jöfnu. Þau eru aðeins gild þegar bæði radix og rök eru jákvæðar tölur. Að auki getur grunnurinn ekki verið jafn 1 eða 0. Eiginleikar lógaritma eru gefnir hér að neðan (með dæmum).
   • log_a(xy) = log_ax + log_ay
     Logaritminn afurð tveggja rökanna „x“ og „y“ er jafn summa lógaritmsins „x“ og lógaritminn „y“ (á sama hátt er summa lógaritmanna jöfn afurð rökanna þeirra ).
     
     Dæmi:
     log₂16 =
     log₂8*2 =
     log₂8 + log₂2
   • log_a(x / y) = log_ax - log_ay
     Logaritminn í kvótanum á rökunum tveimur „x“ og „y“ er jöfn mismuninum á logaritminum „x“ og logaritminum „y“.
     
     Dæmi:
     log₂(5/3) =
     log₂5 - log₂3
   • log_a(x) = r * log_ax
     Hægt er að taka merki „r“ röksemdarinnar „x“ út úr merki logaritmans.
     
     Dæmi:
     log₂(6)
     5 * log₂6
   • log_a(1 / x) = -logg_ax
     Rök (1 / x) = x. Og samkvæmt fyrri eigninni er hægt að taka (-1) úr merki logaritmans.
     
     Dæmi:
     log₂(1/3) = -logg₂3
   • log_aa = 1
     Ef rökin eru jöfn grunninum, þá er slíkur lógaritmi jafn 1 (það er „a“ að krafti 1 er jafnt „a“).
     
     Dæmi:
     log₂2 = 1
   • log_a1 = 0
     Ef rökin eru 1, þá er þessi lógaritmi alltaf 0 (það er „a“ að krafti 0 er 1).
     
     Dæmi:
     log₃1 =0
   • (log_bx / log_ba) = log_ax
     Þetta er kallað að breyta grunn logaritmins. Þegar tveir lógaritmar eru deilt með sama grunni, fæst einn lógaritmi, þar sem grunnurinn er jafngildur rökum deilunnar og rökin eru jöfn rökum arðsins. Það er auðvelt að muna þetta: neðri log rökin lækka (verða grunnur endanlegrar logaritms) og efri log rökin fara upp (verða lokaskrá rökin).
     
     Dæmi:
     log₂5 = (log 5 / log 2)
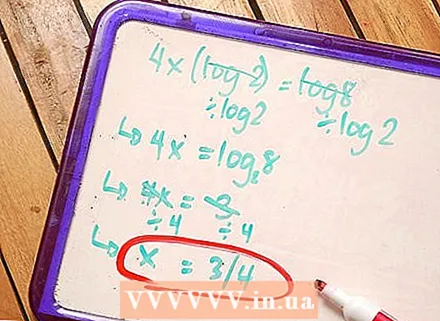5. 5 Æfðu þig í að leysa jöfnur.
   • 4x * log2 = log8 - Skiptu báðum hliðum jöfnunnar með log2.
   • 4x = (log8 / log2) - notaðu skiptingu á grunn logaritmsins.
   • 4x = log₂8 - reikna út verðmæti lógaritmsins.
   • 4x = 3 - Deildu báðum hliðum jöfnunnar með 4.
   • x = 3/4 er síðasta svarið.